Question

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính tan α nếu góc ở tâm chắn cung AB bằng 2α.

Answer 1

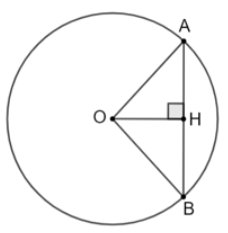
a) Kẻ \( OH \bot AB\).

Ta có \(\Delta AOB\) cân tại O (OA = OB), OH là đường cao nên OH cũng là đường trung tuyên của \(\Delta OAB\)

Suy ra H là trung điểm của AB nên \(AH = HB = 3cm\)

Xét \(\Delta AHO\) vuông tại H, áp dụng định lý Pythagore, ta có:

\(OH = \sqrt{OA^2-AH^2} = \sqrt{5^2-3^2}= 4 (cm)\) 

Vậy khoảng cách từ O đến BC là 4cm.

b) Ta có: \(\widehat{AOB} = 2\alpha \).

OH là đường cao của tam giác AOB cân tại O nên OH cũng là đường phân giác của \(\widehat{AOB}\)

Suy ra \(\widehat {AOH} = \widehat{BOH} = \alpha\)

Tam giác AOH vuông tại H nên ta có:

\(tan\alpha = \frac{AH}{OH} = \frac{3}{4}\)