Question

Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng \(\widehat{IBD}=\widehat{ICA},\widehat{IAC}=\widehat{IDB}\) và IA . IB = IC . ID.

Answer 1

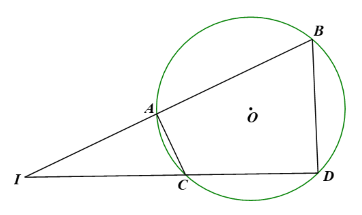
Tứ giác ABDC nội tiếp (O) nên \(\widehat {ABD} + \widehat {ACD} = {180^o}\), mà \(\widehat {ICA} + \widehat {ACD} = {180^o}\) (hai góc kề bù) nên \(\widehat {IBD} = \widehat {ICA}\)

Tứ giác ABDC nội tiếp (O) nên\(\widehat {CAB} + \widehat {CDB} = {180^o}\), mà \(\widehat {CAB} + \widehat {IAC} = {180^o}\) (hai góc kề bù) nên \(\widehat {IAC} = \widehat {IDB}\)

Tam giác IAC và tam giác IDB có:

Góc I chung 

\(\widehat {ICA} = \widehat {IBD}\) (cmt).

Do đo, $\Delta IAC\backsim \Delta IDB\Rightarrow \frac{IA}{IC}=\frac{ID}{IB}\Rightarrow IA.IB=IC.ID$.