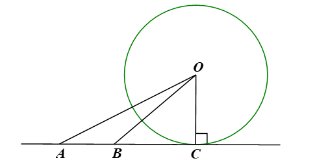
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C.
Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có:
\(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} - A{C^2}\,\,\left( 1 \right)\).
Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có:
\(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} - B{C^2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra \(O{A^2} - A{C^2} = O{B^2} - B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\).
Đúng 0
Bình luận (0)


