Bài 8: Đường tròn
Các câu hỏi tương tự
Vẽ đường tròn tâm O, bán kính R = 3cm. Vẽ một đường kính AB. Vẽ tiếp một dây cung CD (hai điểm C, D không trùng với các điểm A, B và ba điểm C, O, D không thẳng hàng)
a) Đọc tên các cung có các đầu mút là hai trong số các điểm A, B, C, D
b) So sánh độ dàu của hai dây AB và CD
c) Nếu lấy n điểm (phân biệt) trên đường tròn đó ta có được bao nhiêu cung ?
trên đường tròn tâm O, bán kính R lấy 4 điểm phâm biệt A, B, C, D. số cung có các đầu mút là hai trong các điểm đó là
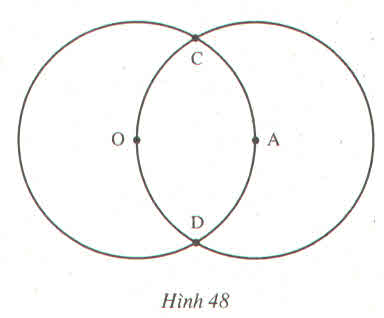
Trên hình 48, ta có hai đường tròn (0;2cm) và (A; 2cm) cắt nhau tại C, D. Điểm A nằm trên đường tròn tâm O
a) Vẽ đường tròn tâm C, bán kính 2cm ?
b) Vì sao đường tròn (C; 2cm) đi qua O, A ?
cho điểm H thuộc đường tròn (c :3,8) thì HC bằng A.1,9CM B.2,8CM C.7,6CM D.3,8CM
Trên hình 49, ta có hai đường tròn (A; 3cm) và (B; 2cm) cắt nhau tại C, D, AB = 4cm. Đường tròn A, B lần lượt cắt đoạn AB tại K, I
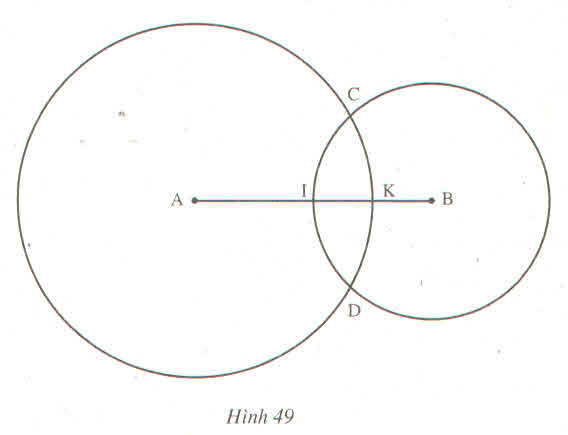
a) Tính CA, CB, DA, DB ?
b) I có phải là trung điểm của đoạn thẳng AB không ?
c) Tính IK ?
Cho đoạn thẳng AB = 4 cm.
a) Dùng compa vẽ đường tròn tâm A, bán kính 2cm.
b) Dùng compa vẽ tất cả những điểm cách B một khoảng 3cm.
c) Có bao nhiêu điểm vừa cách A 2cm, vừa cách B 3cm?
Cho hai điểm A, B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại C và D
a) Tính CA, DB
b) Tại sao đường tròn (B; 1,5cm) cắt đoạn thẳng AB tại trung điểm I của AB ?
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính KB ?
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB 2cm. Vẽ đường tròn (C_1) tâm A, bán kính AB
b) Vẽ đường tròn left(C_2right) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn left(C_1right) là C và G
c) Vẽ đường tròn left(C_3right) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn left(C_1right) là D
d) Vẽ đường tròn left(C_4right) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn left(C_1right) là...
Đọc tiếp
Vẽ hình liên tiếp theo các cách diễn đạt sau :
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (\(C_1\)) tâm A, bán kính AB
b) Vẽ đường tròn \(\left(C_2\right)\) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn \(\left(C_1\right)\) là C và G
c) Vẽ đường tròn \(\left(C_3\right)\) tâm C, bán kính AC. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là D
d) Vẽ đường tròn \(\left(C_4\right)\) tâm D, bán kính AD. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là E
e) Vẽ đường tròn \(\left(C_5\right)\) tâm E, bán kính AE. Gọi các giao điểm mới của đường tròn này với đường tròn \(\left(C_1\right)\) là F
f) Vẽ đường tròn \(\left(C_6\right)\) tâm F, bán kính AF.
g) Vẽ đường tròn \(\left(C_7\right)\) tâm G, bán kính AG
Sau khi vẽ như trên, hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Cho hai điểm A, B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại C và D
a) Tính CA, CB, DA, DB








