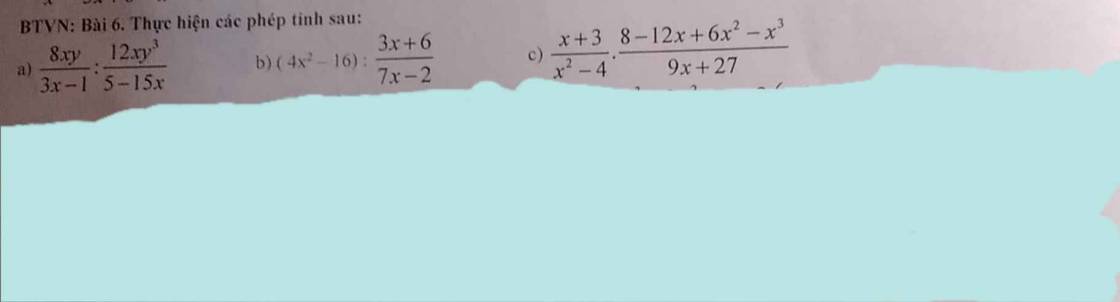a: ĐKXĐ: \(\left\{{}\begin{matrix}y\ne0\\x\notin\left\{\dfrac{1}{3};0\right\}\end{matrix}\right.\)
\(\dfrac{8xy}{3x-1}:\dfrac{12xy^3}{5-15x}\)
\(=\dfrac{8xy}{3x-1}\cdot\dfrac{-15x+5}{12xy^3}\)
\(=-\dfrac{8xy}{12xy^3}\cdot\dfrac{15x-5}{3x-1}\)
\(=\dfrac{-2}{3y^2}\cdot5=-\dfrac{10}{3y^2}\)
b: ĐKXĐ: \(x\notin\left\{-2;2;\dfrac{2}{7}\right\}\)
\(\left(4x^2-16\right):\dfrac{3x+6}{7x-2}\)
\(=4\left(x^2-4\right)\cdot\dfrac{7x-2}{3\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)\left(x+2\right)\cdot\left(7x-2\right)}{3\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)\left(7x-2\right)}{3}\)
c: ĐKXĐ: \(x\notin\left\{-3;2;-2\right\}\)
\(\dfrac{x+3}{x^2-4}\cdot\dfrac{8-12x+6x^2-x^3}{9x+27}\)
\(=\dfrac{x+3}{9x+27}\cdot\dfrac{-x^3+6x^2-12x+8}{x^2-4}\)
\(=\dfrac{x+3}{9\left(x+3\right)}\cdot\dfrac{-\left(x-2\right)^3}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{1}{9}\cdot\dfrac{-\left(x-2\right)^2}{x+2}=\dfrac{-\left(x-2\right)^2}{9\left(x+2\right)}\)