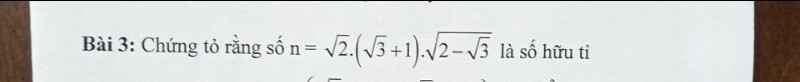Bài 2:
a: \(D=\sqrt{32x+16}+\sqrt{18x+9}-\sqrt{8x+4}+\sqrt{2x+1}\)
\(=4\sqrt{2x+1}+3\sqrt{2x+1}-2\sqrt{2x+1}+\sqrt{2x+1}\)
\(=6\sqrt{2x+1}\)
b: Để D=8 thì 2x+1=9
hay x=4
Bài 1
a) \(\sqrt{12}-\sqrt{27}+\sqrt{48}\)
= \(2\sqrt{3}-3\sqrt{3}-4\sqrt{3
}\)
= \(-5\sqrt{3}\)
b) \(2\sqrt{27}-\sqrt{\dfrac{16}{3}}-\sqrt{48}-\sqrt{8\dfrac{1}{3}}\)
= \(6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}\)
= \(2\sqrt{3}+\dfrac{\sqrt{3}}{3}\)
= \(\dfrac{7\sqrt{3}}{3}\)
c) \(\dfrac{\sqrt{10}-\sqrt{2}}{\sqrt{5}-1}+\dfrac{2-\sqrt{2}}{\sqrt{2}-1}
\)
= \(\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}\)
= \(\sqrt{2}+\sqrt{2}\)
= \(2\sqrt{2}\)