a) điều kiện : \(a>0;a\ne1\)
b) \(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}\left(\dfrac{\sqrt{a}-2}{a-1}-\dfrac{2+\sqrt{a}}{a+2\sqrt{a}+1}\right)\)
\(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}\left(\dfrac{\sqrt{a}-2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{2+\sqrt{a}}{\left(\sqrt{a}+1\right)^2}\right)\)
\(A=\dfrac{\sqrt{a}-2}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{2+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
\(A=\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+1\right)-\left(2+\sqrt{a}\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(A=\dfrac{a+\sqrt{a}-2\sqrt{a}-2-\left(2\sqrt{a}-2+a-\sqrt{a}\right)}{\sqrt{a}\left(a-1\right)}\)
\(A=\dfrac{a+\sqrt{a}-2\sqrt{a}-2-2\sqrt{a}+2-a+\sqrt{a}}{\sqrt{a}\left(a-1\right)}\)
\(A=\dfrac{2\sqrt{a}}{\sqrt{a}\left(a-1\right)}=\dfrac{2}{a-1}\)
c) \(A>0\Leftrightarrow\dfrac{2}{a-1}>0\Leftrightarrow a-1>0\Leftrightarrow a>1\)
vậy \(a>1\) thì \(A>0\)
d) thay \(a=\dfrac{13}{5-2\sqrt{3}}\) vào A ta có \(A=2:\dfrac{13}{5-2\sqrt{3}}=2.\dfrac{5-2\sqrt{3}}{13}=\dfrac{10-4\sqrt{3}}{13}\)

 cách giải bài 5,giúp mình với.
cách giải bài 5,giúp mình với. 


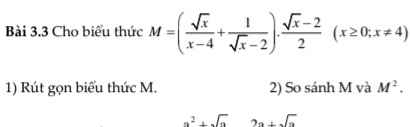






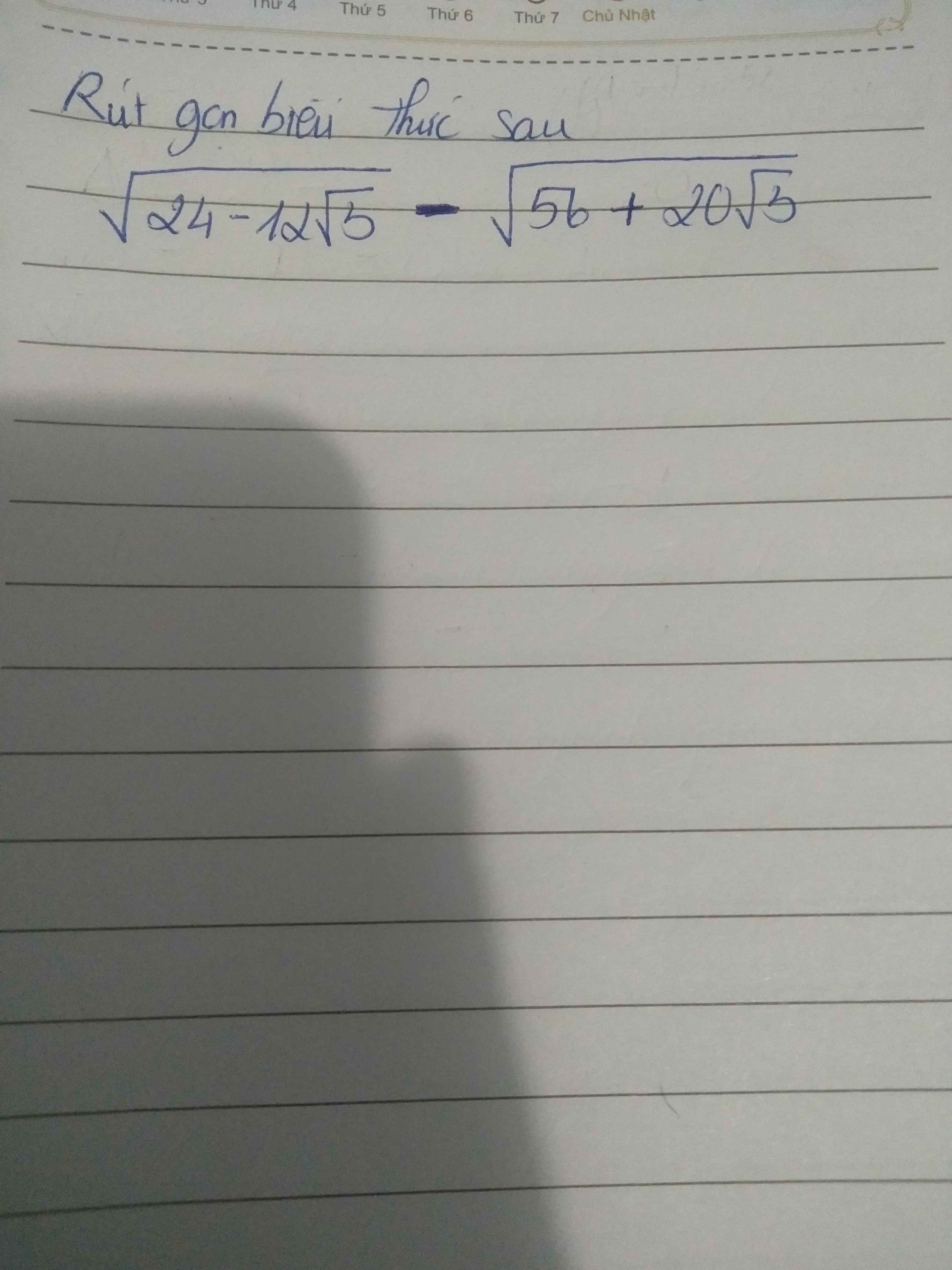



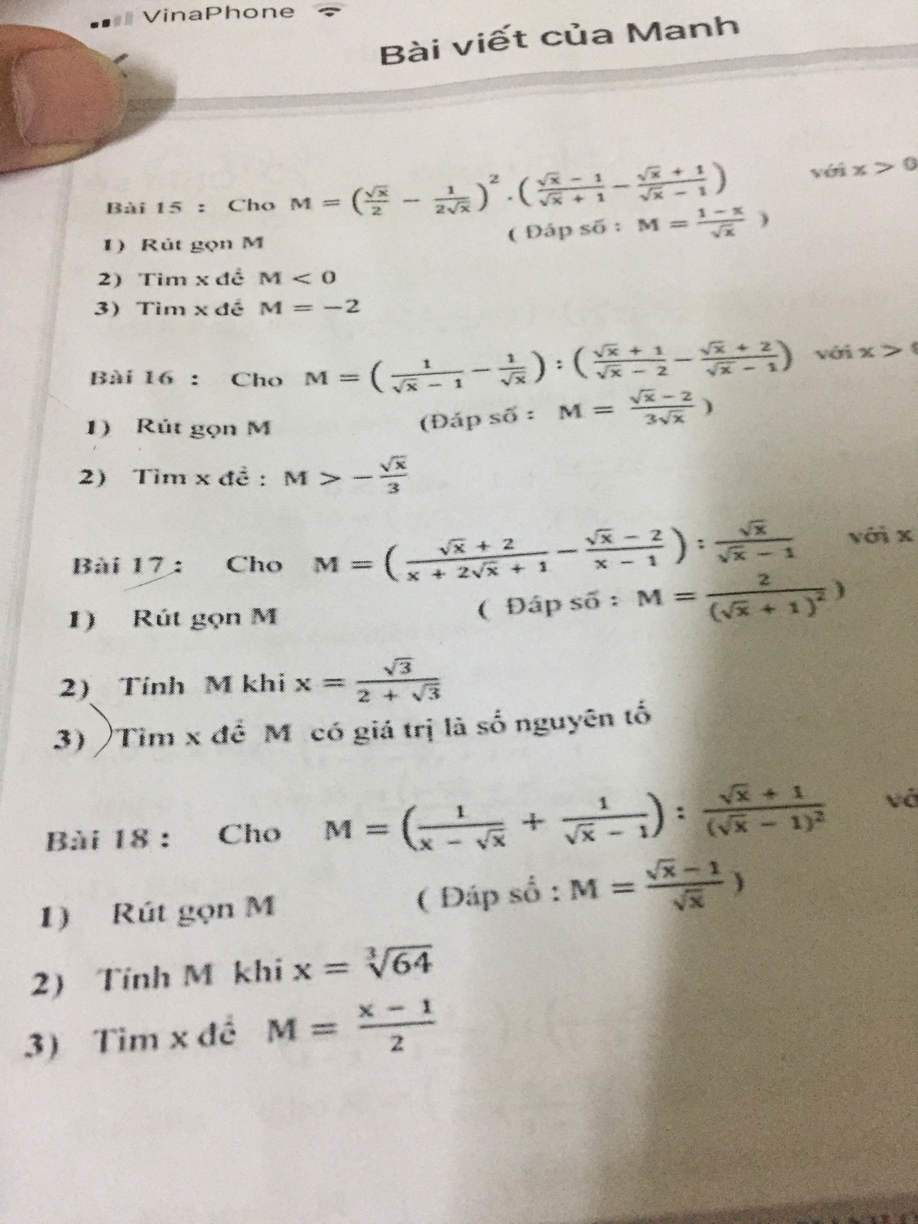 Giải giúp mình bài 17 voi
Giải giúp mình bài 17 voi
 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.