Bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1; 2; 3; 4; 5. Tính xác suất của các biến cố sau:
E: “Rút được tấm thẻ ghi số lẻ”;
F: “Rút được tấm thẻ ghi số chẵn và đồng xu xuất hiện mặt sấp”;
G: “Rút được tấm thẻ ghi số 5 hoặc đồng xu xuất hiện mặt ngửa”.
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là mặt của đồng xu và số ghi trên thẻ.
Không gian mẫu được mô tả dưới dạng bảng như sau:
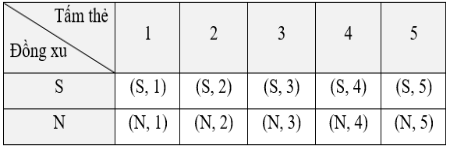
Do đó, số phần tử của không gian mẫu là 10.
Vì An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ nên các kết quả có thể của phép thử là đồng khả năng.
Có 6 kết quả thuận lợi của biến cố E là: (Xấp, 1), (Xấp, 3), (Xấp, 5), (Ngửa, 1), (Ngửa, 3), (Ngửa, 5). Do đó, \(P\left( E \right) = \frac{6}{{10}} = \frac{3}{5}\).
Có 2 kết quả thuận lợi của biến cố F là: (Xấp, 2), (Xấp, 4). Do đó, \(P\left( F \right) = \frac{2}{{10}} = \frac{1}{5}\).
Có 6 kết quả thuận lợi của biến cố G là: (Ngửa, 1), (Ngửa, 2), (Ngửa, 3), (Ngửa, 4), (Ngửa, 5), (Xấp, 5). Do đó, \(P\left( G \right) = \frac{6}{{10}} = \frac{3}{5}\).


