Question

bài 1: một quả cầu rắn co khối lượng m=0,1kg chuyển động với vận tốc v=4m/s trên mặt phẳng nằm ngang sau khi va chạm vào một vách cứng nó bị bật trở lại với cùng vận tốc 4m/s tính độ lớn của lực do vách tác dụng lên quả cầu nếu thời gian va chạm là 0,05s

bài 2: một tên lửa vũ trụ khi bắt đầu rời bệ phóng trong giây đầu tiên đã phụt ra một lượng khí đốt 1300kg vối vận tốc 2500m/s lực đây tên lửa tại thời điểm đó là

bài 3: một chất điểm m bắt đầu trượt không ma sát từ trên mặt phẳng nghiêng xuống gọi α là góc của mặt phẳng nghiêng so với mặt phẳng nằm ngang động lượng chất điểm ở thời điểm t là

Answer 1

bài 2

giải

độ biến thiên động lượng của khí phụt ra trong 1s là

\(\Delta P=1300.2500=325.10^4\left(kg.m/s\right)\)

lực đảy của tên nửa tại thời điểm đó là

\(F=\frac{\Delta P}{\Delta t}=\frac{325.10^4}{1}=325.10^4\left(kg.m/s^2\right)=325.10^4\left(N\right)\)

Answer 2

bài 3

Gia tốc chuyển động trượt không ma sát của vật trên mặt phẳng nghiêng:

a = gsinα.

Động lượng của vật tại thởi điểm t: p = mv = mat = mgsinα.t

Answer 3

bài 1

giải

Quả cầu: \(m=0,1kg;\)\(\overrightarrow{v}=\overrightarrow{-v};\)\(v=4m/s;\)\(\Delta t=0,05s\)

Theo bài 2 thì:

\(\Delta P=-2m.v=-2.0,1.4=-0,8\left(kgm/s\right)\)

\(\Delta P=F.\Delta t\Rightarrow F=\frac{\Delta P}{\Delta t}=\frac{-0,8}{0,05}=-16\left(N\right)\)

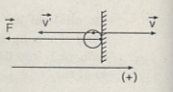Vách tác dụng lên quả cầu lực \(\overrightarrow{F}\) có độ lớn 16N, có phương vuông góc với chiều hướng từ vách ra ngoài.