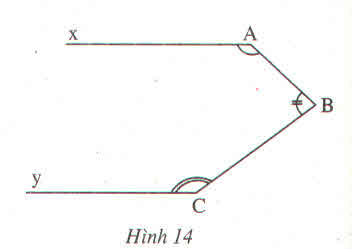
a) Qua B ta kẻ tia \(Bz\) sao cho \(Bz\) // \(Ax.\)
Ta có: \(\widehat{A}+\widehat{B_1}=180^0\) (vì 2 góc trong cùng phía)
Vì \(Bz\) // \(Ax\) (do cách vẽ)
\(Cy\) // \(Ax\left(gt\right)\)
=> \(Bz\) // \(Cy.\)
=> \(\widehat{C}+\widehat{B_2}=180^0\) (vì 2 góc trong cùng phía)
Có: \(\widehat{A}+\widehat{B}+\widehat{C}\)
\(=\widehat{A}+\widehat{B_1}+\widehat{B_2}+\widehat{C}\)
\(=180^0+180^0\)
\(=360^0.\)
Vậy \(\widehat{A}+\widehat{B}+\widehat{C}=360^0.\)
Còn câu b) bạn làm ngược lại thôi nhé.
Chúc bạn học tốt!
trả lời
a) -Kẻ Bz song song với Ax( đã thực hiện trên hình).
Có góc A + góc ABz= 180độ
góc C + góc CBz= 180độ
=> Góc A+ góc B + góc C= 180độ + 180độ = 360độ
b) có Bz song song với Ax=> góc BAx + góc ABz= 180độ
Suy ra góc CBz + góc BCz= 360độ - 180độ= 180độ
=>Bz//Cy (điều phải chứng minh)
CHÚC BẠN MAY MẮN