\(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{49.50}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=1-\dfrac{1}{50}\)
\(=\dfrac{49}{50}\)
\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=1-\dfrac{1}{50}=\dfrac{49}{50}\)
A = \(\dfrac{ 1}{ 1 . 2 } + \dfrac{1}{ 2 . 3 } + ....... + \dfrac{1}{ 49 . 50 }\)
A = \(1 - \dfrac{1}{2} + \dfrac{1 }{2} - \dfrac{1}{ 3 } + \dfrac{1}{3} + ...... - \dfrac{1}{49} + \dfrac{1}{49} - \dfrac{1}{50} \)
A = \(1 - \dfrac{1}{50}\)
A = \(\dfrac{ 50}{50} - \dfrac{1}{50}\)
A = \(\dfrac{49}{50}\)
Vậy \(A = \dfrac{49}{50}\)








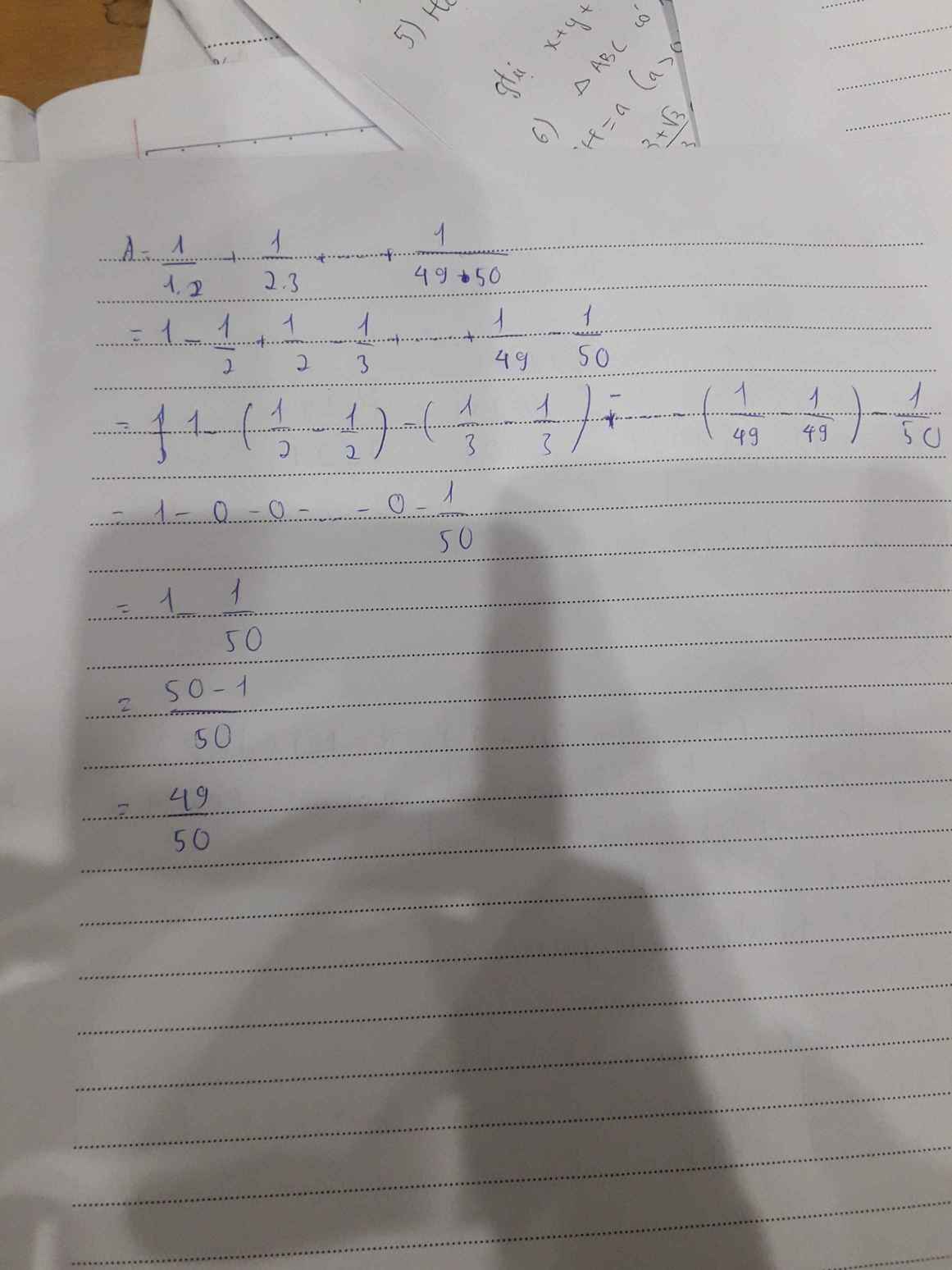



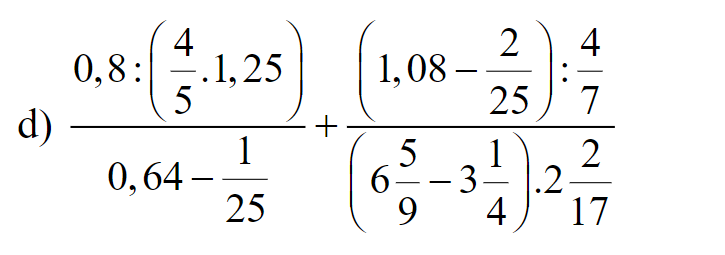



 mọi người giúp em với ạ. em cảm ơn
mọi người giúp em với ạ. em cảm ơn




