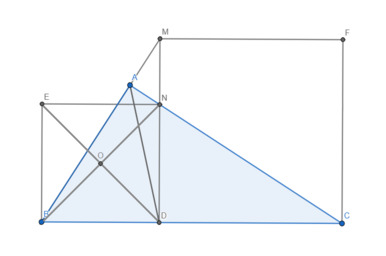
a) ΔABC có AD là phân giác
⇒ \(\dfrac{BD}{AB}\) = \(\dfrac{CD}{AC}\)
ΔDNC đd với ΔABC (g.g) ⇒ \(\dfrac{DN}{AB}\) = \(\dfrac{CD}{AC}\)
⇒ \(\dfrac{BD}{AB}\) = \(\dfrac{DN}{AB}\)
⇒ BD = DN (đpcm)
b) Gọi O là giao điểm của BN và ED
Chứng minh được BDNE là hình chữ nhật
⇒ BN = ED; O là trung điểm của BN, ED
ΔABN vuông tại A có AO là trung tuyến
⇒ AO = \(\dfrac{1}{2}\).BN
⇒ AO = \(\dfrac{1}{2}\).ED
Mà ΔAED có AO là trung tuyến
⇒ ΔAED vuông tại A
⇒ AE ⊥ AD (1)
Chứng minh tương tự ta được: AF ⊥ AD (2)
Từ (1), (2) và theo tiên đề Ơclit
⇒ A, E, F thẳng hàng (đpcm)
















 Giúp mình làm bài này với ạ
Giúp mình làm bài này với ạ
