Bài 5:
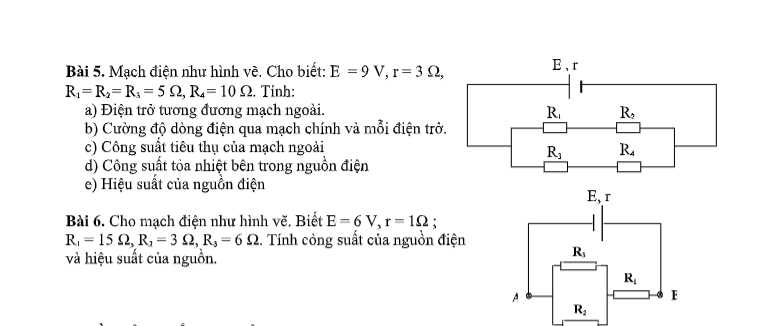
a. MCD: \(\left(R1ntR2\right)//\left(R3ntR4\right)\)
\(\Rightarrow R=\dfrac{R12\cdot R34}{R12+R34}=\dfrac{\left(R1+R2\right)\cdot\left(R3+R4\right)}{\left(R1+R2\right)+\left(R3+R4\right)}=\dfrac{\left(5+5\right)\cdot\left(5+10\right)}{\left(5+5\right)+\left(5+10\right)}=6\Omega\)
b. \(I=\dfrac{\xi}{R+r}=\dfrac{9}{6+3}=1A\)
\(U=U_{12}=U_{34}=IR=1\cdot6=6V\)
\(\rightarrow\left\{{}\begin{matrix}I1=I2=U12:R12=6:\left(5+5\right)=0,6A\\I3=I4=U34:R34=6:\left(5+10\right)=0,4A\end{matrix}\right.\)
c. \(P=UI=6\cdot1=6\)W
Bài 6:
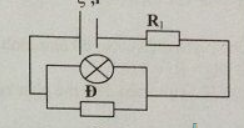
MCD: \(\left(R3//R2\right)ntR1\)
\(\Rightarrow R=R1+\dfrac{R2\cdot R3}{R2+R3}=15+\dfrac{3\cdot6}{3+6}=15,5\Omega\)
\(I=\dfrac{\xi}{R+r}=\dfrac{6}{15,5+1}=\dfrac{4}{11}A\)
\(\rightarrow U=IR=\dfrac{4}{11}\cdot15,5=\dfrac{62}{11}V\)
\(\Rightarrow P=UI=\dfrac{62}{11}\cdot\dfrac{4}{11}=\dfrac{248}{121}\)W
\(\Rightarrow H=\dfrac{U}{\xi}=\dfrac{\dfrac{62}{11}}{6}=\dfrac{31}{33}\%\)