Vẽ các đường parabol sau:
a) \(y = {x^2} - 3x + 2\)
b) \(y = - 2{x^2} + 2x + 3\)
c) \(y = {x^2} + 2x + 1\)
d) \(y = - {x^2} + x - 1\)
Vẽ các đường parabol sau:
a) \(y = {x^2} - 3x + 2\)
b) \(y = - 2{x^2} + 2x + 3\)
c) \(y = {x^2} + 2x + 1\)
d) \(y = - {x^2} + x - 1\)
Từ các parabol đã vẽ ở Bài tập 6.7, hãy cho biết khoảng đồng biến và khoảng nghịch biến của mõi hàm số bậc hai tương ứng.
Thảo luận (1)Hướng dẫn giảia) Hàm số \(y = {x^2} - 3x + 2\)nghịch biến trên khoảng \(\left( { - \infty ;\frac{3}{2}} \right)\); đồng biến trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\)
b) Hàm số \(y = - 2{x^2} + 2x + 3\) đồng biến trên khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\); nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
c) Hàm số \(y = {x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\); đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\)
d) Hàm só \(y = - {x^2} + x - 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\); nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
(Trả lời bởi Hà Quang Minh)
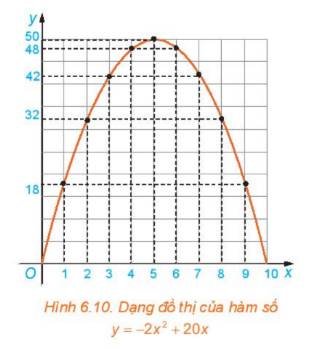
Xét hàm số \(y = S(x) = - 2{x^2} + 20x(0 < x < 10)\)
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số \(y = - 2{x^2} + 20x\)trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị \(y = - 2{x^2} + 20x\) có giống với đồ thị của hàm số \(y = - 2{x^2}\) hay không?
b) Quan sát dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\) trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.
c) Thực hiện phép biến đổi \(y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\) Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
Thảo luận (1)Hướng dẫn giảia) Ta có đồ thị hàm số \(y = - 2{x^2}\)
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\)giống với dạng đồ thị \(y = - 2{x^2}\)
b) Tọa độ điểm cao nhất là \(\left( {5;50} \right)\)
c) Ta có: \(S(x) = y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\)
\({(x - 5)^2} \ge 0 \Rightarrow - 2{(x - 5)^2} + 50 \le 50 \Rightarrow S(x) \le 50\)
Do đó diện tích lớn nhất của mảnh đất rào chắn là 50 \(({m^2})\) khi x = 5.
(Trả lời bởi Hà Quang Minh)
Bạn Nam đứng dưới chân cầu vượt ba tầng ở nút giao ngã ba Huế, thuộc thành phố Đà Nẵng để ngắm cảnh cầu vượt (H.6.13) Biết rằng trụ tháp cầu có dạng đường parabol, khoảng cách giữa hai chân trụ tháp khoảng 27 m, chiều cao của trụ tháp tính từ điêm trên mặt đất cách chân trụ tháp 2,26 m là 20 m. Hãy giúp bạn Nam ước lượng ộ cao của đỉnh trụ tháp cầu (so với mặt đất).

Thảo luận (1)Hướng dẫn giảiĐồ thị \(y = a{x^2} + bx\) đi qua điểm có tọa độ (2,26;20) và (27;0)
Nên ta có \(\begin{array}{l}a.{(2,26)^2} + b.2,26 = 20\\a{.27^2} + b.27 = 0\end{array}\)\( \Leftrightarrow \)\(\begin{array}{l}a \approx - 0,358\\b \approx 9,666\end{array}\)
Do đó ta có hàm số \(y = - 0,358{x^2} + 9,666x\)
Tọa độ đỉnh là \(x = \frac{{ - b}}{{2a}} = 13,5\); \(y = 65,2455\)
Vậy độ cao của đỉnh trụ tháp cầu so với mặt đất khoảng 65,2455m
(Trả lời bởi Hà Quang Minh)
Tương tự HĐ2, ta có dạng đồ thị của một số hàm số bậc hai sau.
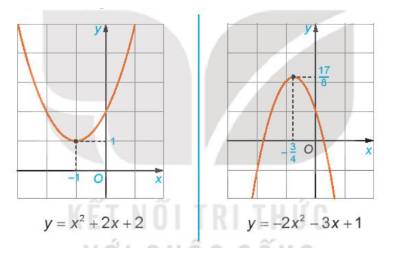
Từ các đồ thị trên, hãy hoàn thành bảng sau đây.
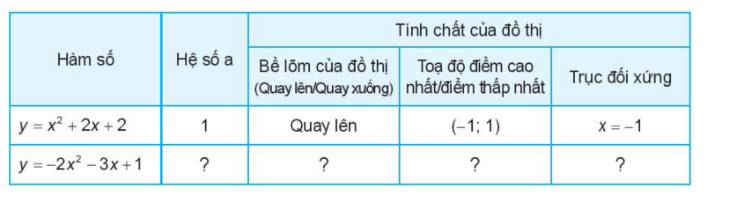
Thảo luận (1)Hướng dẫn giải
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2};h,t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
Thảo luận (1)Hướng dẫn giảia) Để viên bi chạm đất thì \(\begin{array}{l}h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\\ \Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\end{array}\)
Do \(t \ge 0\) nên t=2(s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\)
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\)
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\)
(Trả lời bởi Hà Quang Minh)
Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^4} + 3{x^2} + 2\)
B. \(y = \frac{1}{{{x^2}}}\)
C. \(y = - 3{x^2} + 1\)
D. \(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\)\(\)
Thảo luận (1)Hướng dẫn giảiHàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai.
(Trả lời bởi Hà Quang Minh)
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\)là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
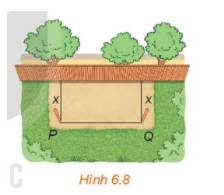
Thảo luận (1)Hướng dẫn giảia) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)
(Trả lời bởi Hà Quang Minh)
Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.
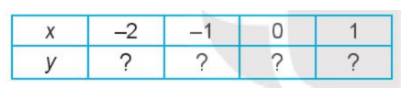
Thảo luận (1)Hướng dẫn giảia) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y = (x - 1)(2 - 3x) ta có:
(Trả lời bởi Hà Quang Minh)
Vẽ parabol \(y = 3{x^2} - 10x + 7\). Từ đó tìm khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số \(y = 3{x^2} - 10x + 7\).
Thảo luận (1)Hướng dẫn giảiVẽ đồ thi \(y = 3{x^2} - 10x + 7\)
- Có đỉnh \(\)\(I\left( {\frac{5}{3}; - \frac{4}{3}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{5}{3}\)
- Đi qua điểm \((0;7);\left( {1;0} \right)\)
- Hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{3}} \right)\); đồng biến trên khoảng \(\left( {\frac{5}{3}; + \infty } \right)\)
- Giá trị nhỏ nhất của hàm số là tại điểm có tọa độ \(\left( {\frac{5}{3}; - \frac{4}{3}} \right)\)
(Trả lời bởi Hà Quang Minh)