Một quyển sách đặt trên mặt bàn nghiêng và được thả cho trượt xuống. Cho biết góc nghiêng α = 30o so với phương ngang và hệ số ma sát giữa quyển sách và mặt bàn là µ = 0,27. Lấy g = 9,8 m/s2. Gia tốc của quyển sách và quãng đường đi được của nó sau 2 s lần lượt là
2,6 m/s2 và 5,2 m. 2,35 m/s2 và 4,7 m. 2,2 m/s2 và 4,4 m. 2,85 m/s2 và 5,7 m. Hướng dẫn giải: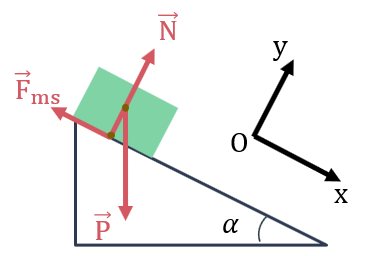
Các lực tác dụng lên quyển sách: trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{N}\), lực ma sát trượt \(\overrightarrow{F}_{ms}\)
Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy ta được:
\(\left\{{}\begin{matrix}F_x=P_x-F_{ms}=mgsin\alpha-\mu N=ma\\F_y=N-P_y=N-mgcos\alpha=0\end{matrix}\right.\)
\(\Rightarrow N=mgcos\alpha\)
Thay vào phương trình chuyển động theo trục Ox ta có:
\(mgsin\alpha-\mu mgcos\alpha=ma\Rightarrow a=g\left(sin\alpha-\mu cos\alpha\right)\)
Thay số ta được:
\(a=g\left(sin\alpha-\mu cos\alpha\right)=9,8\left(sin30^o-0,27.cos30^o\right)=2,6\) m/s2
Quãng đường đi được sau 2 s:
\(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.2,6.2^2=5,2\) m

