Một cái thùng khối lượng m = 12 kg đặt trên sàn nhà. Người ta kéo thùng bằng một lực \(\overrightarrow{F}\) hướng chếch lên trên và hợp với phương nằm ngang một góc \(\alpha=25^o\). Thùng chuyển động đều trên sàn nhà. Biết hệ số ma sát trượt giữa thùng và sàn nhà là 0,3. Lấy g = 9,8 m/s2. Độ lớn của lực \(\overrightarrow{F}\) là
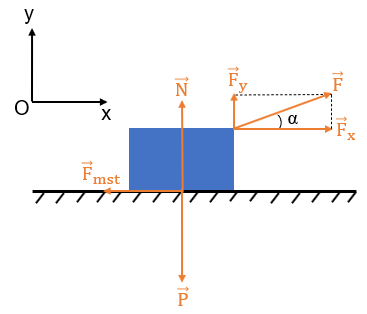
Thùng chịu tác dụng của các lực: lực kéo \(\overrightarrow{F}\), trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{N}\) và lực ma sát trượt \(\overrightarrow{F}_{mst}\).
Chọn hệ trục tọa độ Oxy như hình vẽ.
Phân tích lực \(\overrightarrow{F}\) thành hai lực thành phần vuông góc: \(\left\{{}\begin{matrix}F_x=Fcos\alpha\\F_y=Fsin\alpha\end{matrix}\right.\)
Vì thùng chuyển động đều nên gia tốc \(\overrightarrow{a}=0\). Theo Định luật 2 Newton ta có:
\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}_{mst}=0\) (*)
Chiếu (*) lên trục Ox ta có: \(F_x-F_{mst}=0\Rightarrow Fcos\alpha-\mu N=0\) (1)
Chiếu (*) lên trục Oy ta có: \(F_y-P+N=0\Rightarrow N=mg-Fsin\alpha\) (2)
Thay (2) vào (1) ta có: \(Fcos\alpha-\mu\left(mg-Fsin\alpha\right)=0\)
\(\Rightarrow F=\dfrac{\mu mg}{cos\alpha+\mu sin\alpha}=\dfrac{0,3.12.9,8}{cos25^o+0,3.sin25^o}=34,1\) N

