Cho tứ diện ABCD có \(AB=CD=a,IJ=\dfrac{a\sqrt{3}}{2}\) (\(I,J\) lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là
\(60^o\)\(40^o\)\(50^o\)\(30^o\)Hướng dẫn giải: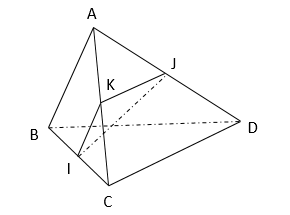
Gọi K là trung điểm của AB.
Góc giữa hai đường thẳng AB và CD bằng góc giữa KI và KJ.
Áp dụng định lý Cô-sin ta có:
\(cos\widehat{IKJ}=\dfrac{KI^2+KJ^2-IJ^2}{2KI.KJ}\) \(=\dfrac{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2-\left(\dfrac{a\sqrt{3}}{2}\right)^2}{2.\dfrac{a}{2}.\dfrac{a}{2}}=-\dfrac{1}{2}\).
Suy ra góc giữa hai đường thẳng KI và KJ bằng \(60^o\) hay góc giữa AB và CD bằng \(60^o\).

