Ôn tập chương Hình lăng trụ đứng. Hình chóp đều.

1. Quan hệ song song, vuông góc trong không gian

- Trong không gian, 2 đường thẳng phân biệt \(a\) và \(b\) có thể

+) Cắt nhau: Nếu chúng cùng nằm trong một mặt phẳng và có một điểm chung;

+) Vuông góc: Nếu chúng cùng nằm trong một mặt phẳng và tạo với nhau một góc \(90^0\);

+) Song song: Nếu chúng cùng nằm trong một mặt phẳng và không có điểm chung;

+) Không cùng thuộc một mặt phẳng nào.

- Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

- Đường thẳng song song với mặt phẳng: Nếu một đường thẳng \(a\) không nằm trong mặt phẳng \(\left(\alpha\right)\) mà nó song song với một đường thẳng \(b\) thuộc mặt phẳng \(\left(\alpha\right)\) thì ta nói đường thẳng \(a\) song song với mặt phẳng \(\left(\alpha\right)\). Kí hiệu: \(a\) // \(mp\left(\alpha\right)\)

 - Hai mặt phẳng song song: Nếu mặt phẳng \(\left(\alpha\right)\) chứa hai đường thẳng phân biệt lần lượt song song với hai đường thẳng phân biệt thuộc mặt phẳng \(\left(\beta\right)\) thì ta nói hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) song song với nhau. Kí hiệu: \(mp\left(\alpha\right)\) // \(mp\left(\beta\right)\)

- Nhận xét:

+ Nếu một đường thẳng song song với một mặt phẳng thì chúng không có điểm chung;

+ Hai mặt phẳng song song thì không có điểm chung; 

- Hai mặt phẳng phân biệt có một điểm chung thì chúng có chung một đường thẳng đi qua điểm đó. Ta nói hai mặt phẳng đó cắt nhau.

- Đường thẳng vuông góc với mặt phẳng: Nếu đường thẳng \(a\) vuông góc với 2 đường thẳng cắt nhau \(b\) và \(c\) thuộc mặt phẳng \(\left(\alpha\right)\) thì ta nói đường thẳng \(a\) vuông góc với mặt phẳng \(\left(\alpha\right)\). Kí hiệu: \(a\perp mp\left(\alpha\right)\).

- Nhận xét: Nếu một đường thẳng vuông góc với một mặt phẳng tại điểm \(A\) thì nó vuông góc với tất cả các đường thẳng đi qua \(A\) thuộc mặt phẳng đó.

- Hai mặt phẳng vuông góc: Mặt phẳng \(\left(\alpha\right)\) chứa một đường thẳng \(a\) vuông góc với mặt phẳng \(\left(\beta\right)\) thì ta nói mặt phẳng \(\left(\alpha\right)\) vuông góc với mặt phẳng \(\left(\beta\right)\). Kí hiệu: \(mp\left(\alpha\right)\perp mp\left(\beta\right)\)

2. Hình hộp chữ nhật. Hình lập phương

- Hình hộp chữ nhật là hình có 6 mặt đều là hình chữ nhật.

- Hình lập phương có 6 mặt đều là hình vuông. Hình lập phương là một hình hộp chữ nhật đặc biệt.

- Hình hộp chữ nhật có: 6 mặt, 8 đỉnh, 12 cạnh.

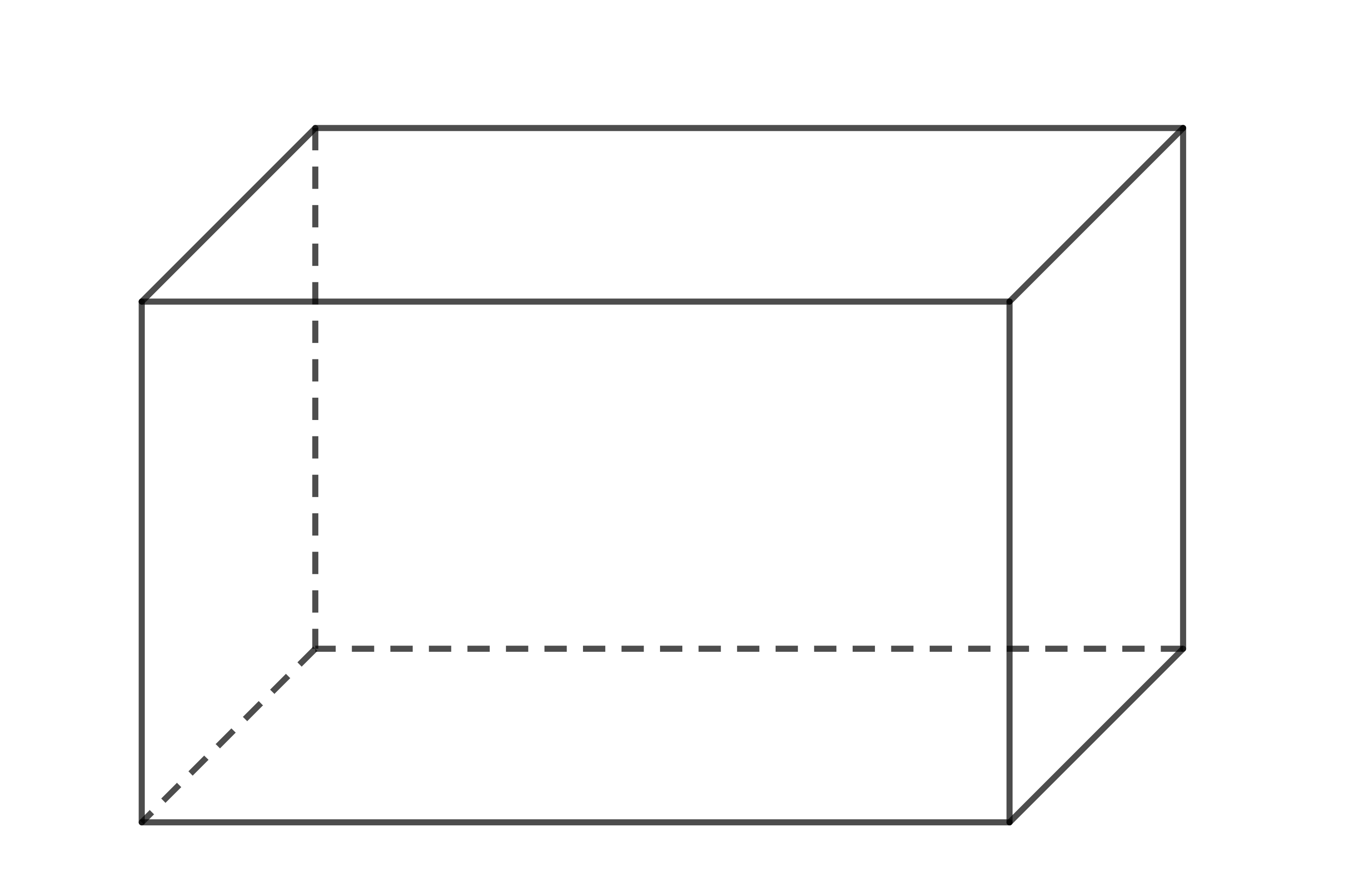
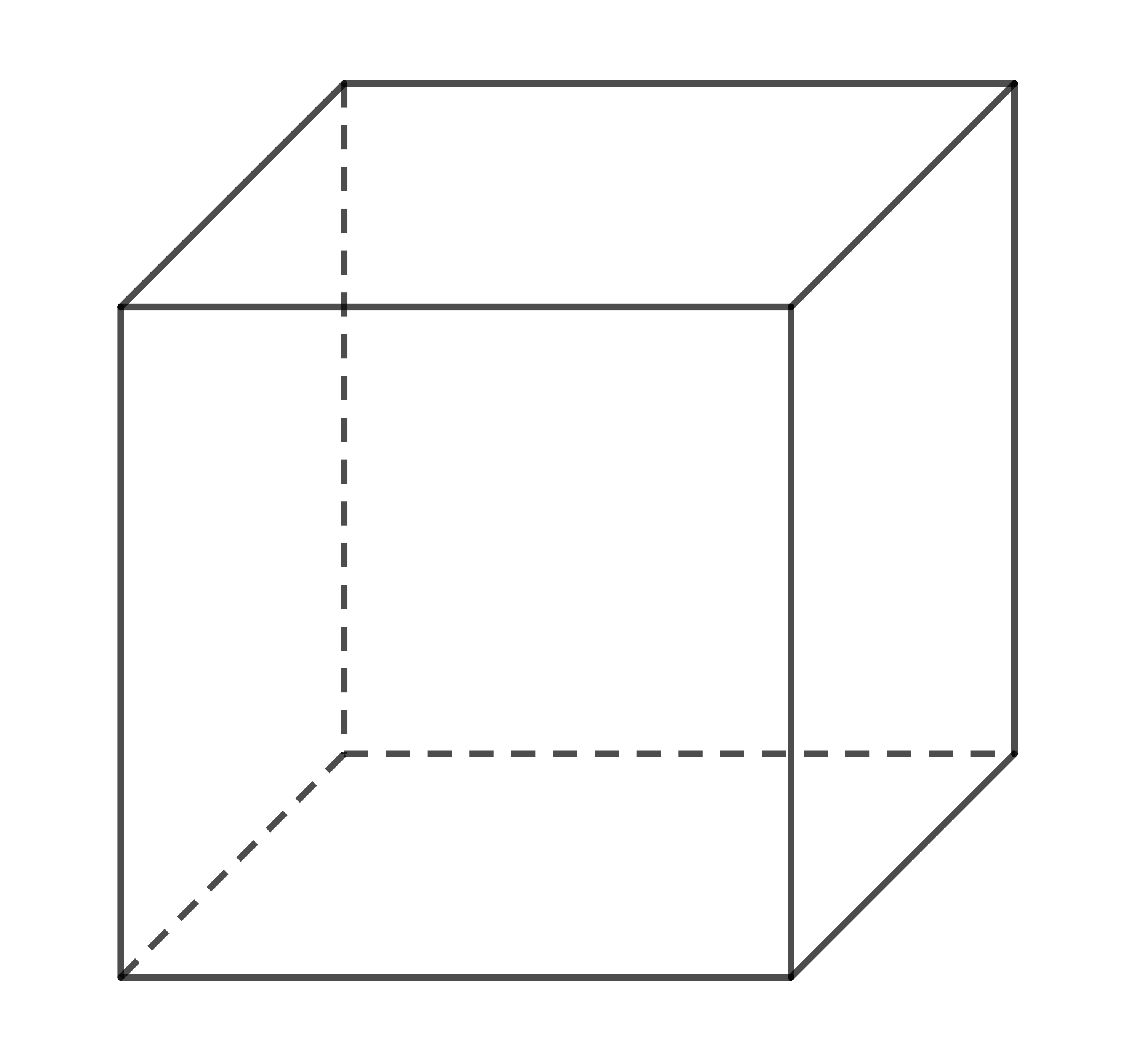
- Diện tích xung quanh của hình hộp chữ nhật bằng tích của chu vi đáy và chiều cao: \(S_{xq}=2p.h\)

      Trong đó: \(p\) là nửa chu vi đáy;

                      \(h\) là chiều cao.

- Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích đáy: \(S_{tp}=S_{xq}+S_đ\)

- Thể tích hình hộp chữ nhật: Nếu một hình hộp chữ nhật có 3 kích thước lần lượt là \(a,b,c\) thì thể tích hình hộp chữ nhật là: \(V=a.b.c\)

- Thể tích hình lập phương cạnh \(a\) là: \(V=a^3\)

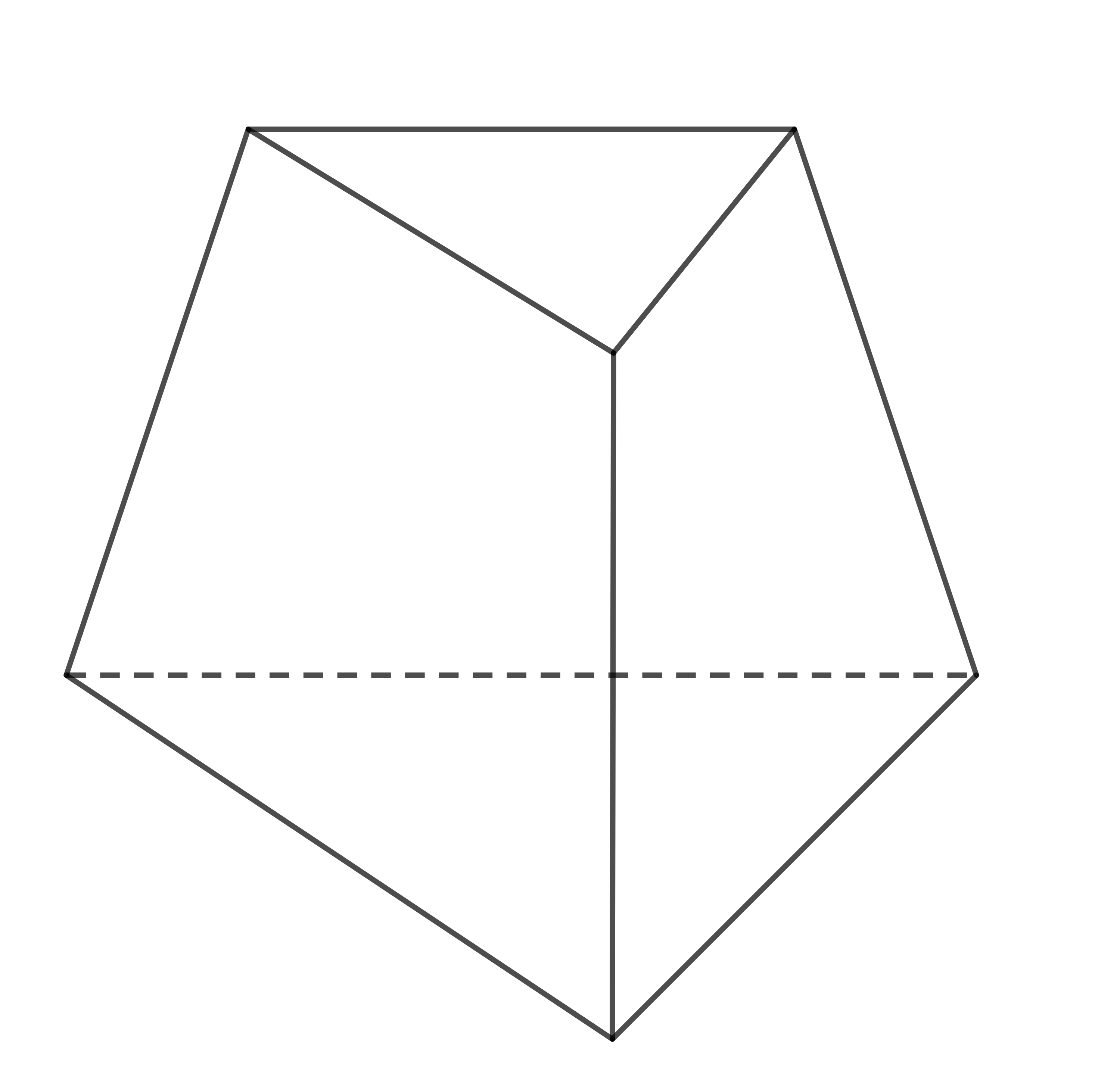
3. Hình lăng trụ đứng

- Hình lăng trụ đứng là hình có đáy là một đa giác, các mặt bên là các hình chữ nhật.

- Hình lăng trụ đứng là hình lăng trụ có đáy là đa giác đều.

- Hình hộp chữ nhật, hình lập phương cũng là một hình lăng trụ đứng.

- Tên gọi của hình lăng trụ đứng phụ thuộc vào số cạnh của đa giác đáy.

Ví dụ: Hình lăng trụ đứng có đáy là tứ giác, ta gọi là lăng trụ đứng tứ giác;

          Hình lăng trụ đứng có đáy là ngũ giác, ta gọi là lăng trụ đứng ngũ giác;

          Hình lăng trụ đứng có đáy là tam giác, ta gọi là lăng trụ đứng tam giác; ...

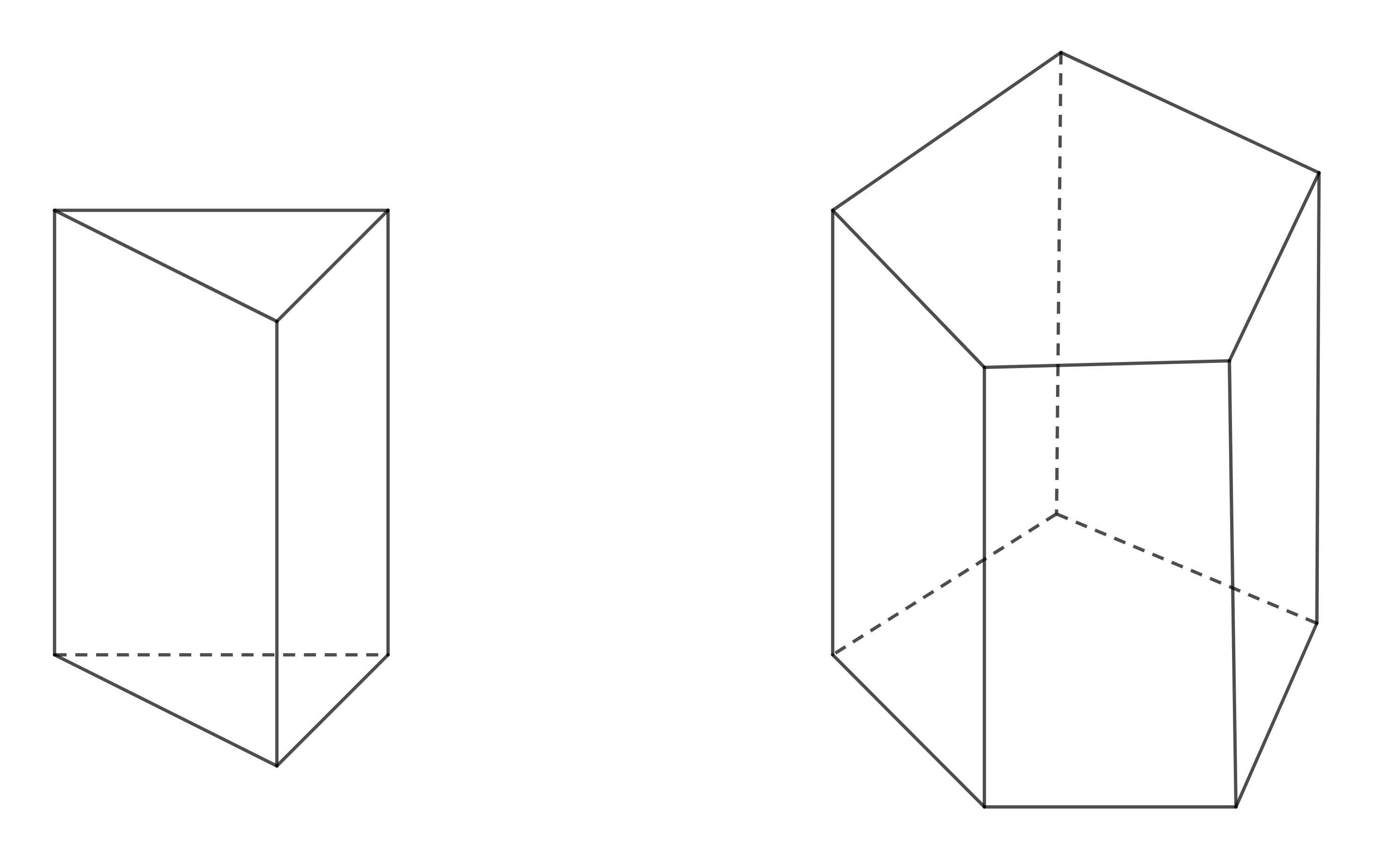
- Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao: \(S_{xq}=2p.h\)

      Trong đó: \(p\) là nửa chu vi đáy;

                      \(h\) là chiều cao.

- Diện tích toàn phần của hình lăng trụ đứng bằng diện tích xung quanh cộng với diện tích đáy: \(S_{tp}=S_{xq}+S_đ\)

- Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao: \(V=S.h\)

      Trong đó: \(S\) là diện tích đáy;

                      \(h\) là chiều cao.

4. Hình chóp đều và hình chóp cụt đều

- HÌnh chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh. Đỉnh đó gọi là đỉnh của hình chóp.

- Tên gọi của hình chóp thuộc vào số cạnh của đa giác đáy.

Ví dụ: Hình chóp đều có đáy là tứ giác, ta gọi là chóp tứ giác đều;

          Hình chóp đều có đáy là ngũ giác, ta gọi là chóp ngũ giác đều;

          Hình chóp đều có đáy là tam giác, ta gọi là chóp tam giác đều; ...

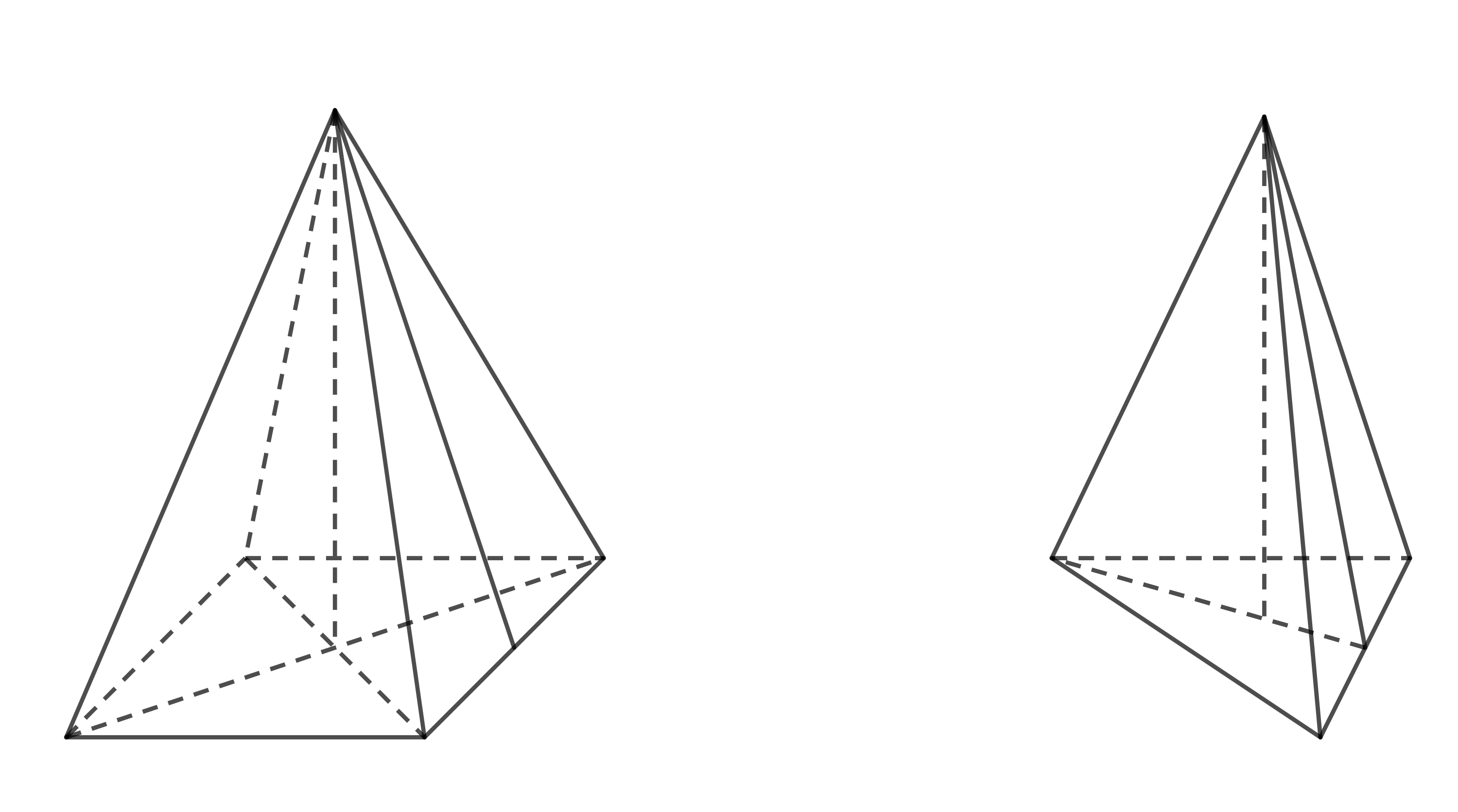
- Diện tích xung quanh của hình chóp đều bằng nửa chu vi đáy nhân với trung đoạn: \(S_{xq}=p.d\)

     Trong đó: \(p\) là nửa chu vi đáy;

                     \(d\) là độ dài trung đoạn của hình chóp đều.

- Diện tích toàn phần bằng diện tích xung quanh cộng với diện tích đáy: \(S_{tp}=S_{xq}+S_đ\)

- Thể tích hình chóp đều: \(V=\dfrac{1}{3}.S.h\)

     Trong đó: \(S\) là diện tích đáy;

                     \(h\) là chiều cao.

- Cắt hình chóp đều bằng một mặt phẳng song song với mặt phẳng đáy, phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy là một hình chóp cụt đều.