Ôn tập chương Đường thẳng vuông góc. Đường thẳng song song

1. Hai góc đối đỉnh:

- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Ví dụ: Trong hình vẽ dưới đây:

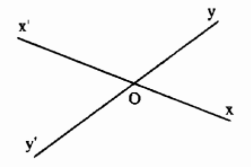
Hai góc \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) là hai góc đối đỉnh vì cạnh \(Ox\) là tia đối của cạnh \(Ox'\), cạnh \(Oy\) là tia đối của cạnh \(Oy'\).

- Tính chất: Hai góc đối đỉnh thì bằng  nhau.

Ví dụ:

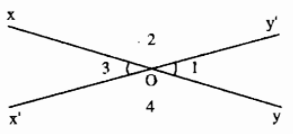
Hai góc \(\widehat{O_1}\) và \(\widehat{O_3}\) là hai góc đối đỉnh. Ta có \(\widehat{O_1}=\widehat{O_3}\).

2. Hai đường thẳng vuông góc

- ĐỊnh nghĩa: Hai đường thẳng \(xx'\) và \(yy'\) cắt nahu và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc và được kí hiệu là \(xx'\perp yy'\).

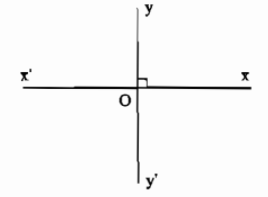
- Khi \(xx'\) và \(yy'\) là hai đường thẳng vuông góc và cắt nhau tại \(O\) ta còn nói: Đường thẳng \(xx'\) vuông góc với đường thẳng \(yy'\) tại \(O\); hoặc đường thẳng \(yy'\) vuông góc với đường thẳng \(xx'\) tại \(O\); hoặc hai đường thẳng \(xx'\)và \(yy'\) vuông góc với nhau tại \(O\).

- Ta thừa nhận tính chất sau: Có một và chỉ một đường thẳng \(a'\) đi qua điểm \(O\) và vuông góc với đường thẳng \(a\) cho trước.

- Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng đó tại trung điểm của nó.

Ví dụ:

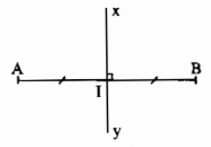
\(I\) là trung điểm đoạn \(AB\), đường thẳng \(xy\) vuông góc với \(AB\) tại \(I\). Ta nói đường thẳng \(xy\) là đường trung trực của đoạn thẳng \(AB\).

Khi đó ta còn nói: Hai điểm \(A\) và \(B\) đối xứng nhau qua đường thẳng \(xy\).

3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng

- Cho một đường thẳng \(a\) cắt hai đường thẳng \(b\), \(c\) (như hình vẽ)

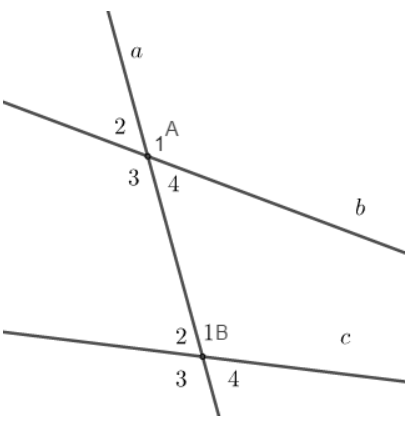
Các cặp góc \(\widehat{A_3}\) và \(\widehat{B_1}\), \(\widehat{A_4}\) và \(\widehat{B_2}\) là các cặp góc so le trong.

Các cặp góc \(\widehat{A_1}\) và \(\widehat{B_1}\), \(\widehat{A_2}\) và \(\widehat{B_2}\), \(\widehat{A_3}\) và \(\widehat{B_3}\), \(\widehat{A_4}\) và \(\widehat{B_4}\) là các cặp góc đồng vị.

- Ta có tính chất sau: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\), \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

+ Hai góc so le trong còn lại bằng nhau.

+ Hai góc đồng vị bằng nhau.

Ví dụ (hình vẽ):

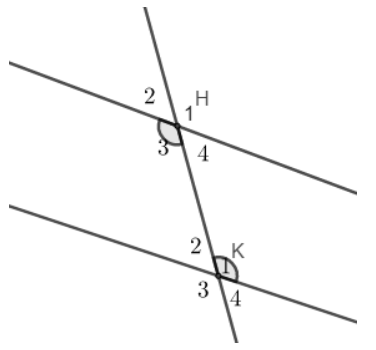
Ta có: Cặp góc so le trong \(\widehat{H_3}=\widehat{K_1}\)

\(\Rightarrow\) Cặp góc so le trong còn lại \(\widehat{H_4}=\widehat{K_2}\)

Các cặp góc đồng vị: \(\widehat{H_1}=\widehat{K_1}\), \(\widehat{H_2}=\widehat{K_2}\), \(\widehat{H_3}=\widehat{K_3}\), \(\widehat{H_4}=\widehat{K_4}\).

4. Hai đường thẳng song song

- Hai đường thẳng song song là hai đường thẳng không có điểm chung.

- Hai đường thẳng phân biệt thì hoặc cắt nahu hoặc song song.

- Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\), \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì \(a\) và \(b\) song song với nhau.

Ví dụ: 

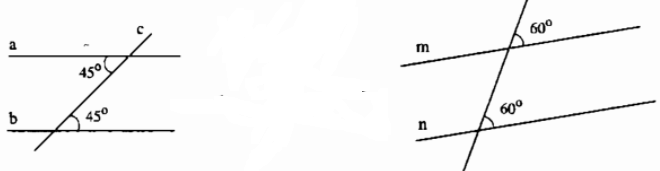
- Khi hai đường thẳng \(a\), \(b\) song song với nhau được kí hiệu là : \(a\)//\(b\).

5. Tiên đề Ơ-clit về hai đường thẳng song song

- Nội dung tiên đề: Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Ví dụ (hình vẽ):

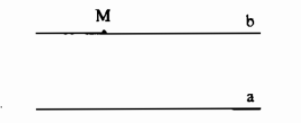
Điểm \(M\) nằm ngoài đường thẳng \(a\), đường thẳng \(b\) đi qua \(M\) và song song với \(a\) là duy nhất.

- Tính chất của hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng song song thì:

+ Hai góc so le trong bằng nhau.

+ HaI góc đồng vị bằng nhau.

+ Hai góc trong cùng phía bù nhau.

6. Từ vuông góc đến song song

- Quan hệ giữa tính vuông góc với tính song song:

+ Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.

Ví dụ: \(a\perp c\) , \(b\perp c\) \(\Rightarrow\) \(a\) // \(b\)

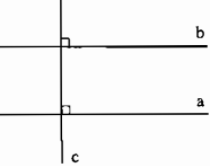
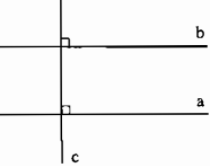
+ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.

Ví dụ: \(a\)//\(b\), \(a\perp c\)  \(\Rightarrow\) \(b\perp c\)

- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

Ví dụ: \(d'\)//\(d\) và \(d''\)//\(d\) \(\Rightarrow\) \(d'\)//\(d''\)

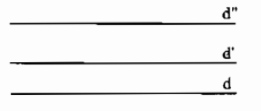
Khi đó ba đường thẳng \(d\), \(d'\), \(d''\) song song với nhau từng đôi một ta nói ba đường thẳng ấy song song với nhau và kí hiệu là \(d\)//\(d'\)//\(d''\).

7. Định lí

- Định lí là một khẳng định suy ra từ những khẳng định được coi là đúng.

Ví dụ: "Hai góc đối đỉnh thì bằng nhau" là một định lí.

- Giả thiết của định lí (viết tắt là GT) là điều đã cho. Kết luận của định lí l(viết tắt là KL) à điều phải suy ra.

- Khi định lí được viết dưới dạng "Nếu...thì...", phần nằm giữa từ "Nếu" và từ "thi" là phần giả thiết, phần nằm sau từ "thì" là kết luận.

- Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.