Luyện tập chung
Nội dung lý thuyết
Một số ví dụ
Ví dụ 1. Tính giá trị của biểu thức
a) \(200+\left[\left(3^4-24\right)+12^0.3\right]-14.2^2\);
b) \(220-8^2+45:3^2\);
c) \(125:5+28.11^0\).
Giải:
a) \(200+\left[\left(3^4-24\right)+12^0.3\right]-14.2^2\)
\(=200+\left[\left(81-24\right).1.3\right]-14.4\\ =200+171-56\\ =371-56=315.\)
Vậy biểu thức có giá trị bằng 315.
b) \(220-8^2+45:3^2\)
\(=220-64+45:9\)
\(=156+5\)
\(=161.\)
Vậy biểu thức có giá trị bằng 161.
c) \(125:5+28.11^0\)
\(=25+28.1\)
\(=25+28=53\).
Vậy biểu thức có giá trị bằng 53.
Ví dụ 2. Tìm \(x\), biết:
a) \(2x-3.5^2=45:\left(41-5.2^3\right)\);
b) \(56-x=\left\{128-\left[110:\left(2^3.17-9^2\right)\right]\right\}:3^2\);
c) \(2x+2.5^2=231:3^1+121:11\).
Giải:
a) \(2x-3.5^2=45:\left(41-5.2^3\right)\)
\(2x-3.25=45:\left(41-40\right)\)
\(2x-75=45\)
\(2x=45+75\)
\(x=\dfrac{45+75}{2}\)
\(x=60\).
b) \(56-x=\left\{128-\left[110:\left(2^3.17-9^2\right)\right]\right\}:3^2\)
\(56-x=\left\{128-\left[110:\left(8.17-81\right)\right]\right\}:9\)
\(56-x=\left\{128-\left[110:55\right]\right\}:9\)
\(56-x=\left\{128-2\right\}:9\)
\(56-x=126:9\)
\(56-x=14\\ x=56-14\\ x=42.\)
c) \(2x+2.5^2=231:3^1+121:11\)
\(2x+2.25=231:3+11\\ 2x+50=77+11\\ 2x+50=88\\ 2x=38\\ x=19.\)
Ví dụ 3. Viết kết quả các phép tính sau dưới dạng một lũy thừa.
a) \(5^6:5^2\);
b) \(10^5.125.8\);
c) \(7^5.7^3:7^4\).
Giải:
a) \(5^6:5^2=5^{6-2}=5^4.\)
b) \(10^5.125.8=10^5.1000=10^5.10^3=10^{5+3}=10^8\).
c) \(7^5.7^3:7^4=7^{5+3}:7^4=7^8:7^4=7^{8-4}=7^4\).
Ví dụ 4. Viết biểu thức tính diện tích toàn phần của hình hộp chữ nhật sau theo a, b và c. Tính giá trị của biểu thức đó khi a = 6 cm; b = 10 cm; c = 5 cm.
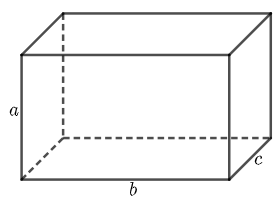
Giải:
Diện tích toàn phần của hình chữ nhật là: 2bc + 2ac + 2ab (cm2).
Khi a = 6 cm; b = 10 cm; c = 5 cm ta có diện tích toàn phần là:
2.10.5 + 2.6.5 + 2.6.10 = 280 (cm2).
@919158@@919239@@919311@