Bài tập cuối chương V

1. HÌNH CÓ TRỤC ĐỐI XỨNG

Các hình dưới đều có chung tính chất: Có một đường thẳng d chia hình thành hai phần mà nếu "gấp" hình theo đường thẳng d thì hai phần đó chồng khít lên nhau.

Những hình như thế gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

Một số hình có trục đối xứng trong thực tế

2. TRỤC ĐỐI XỨNG CỦA MỘT SỐ HÌNH PHẲNG

Hình tròn, hình thang cân, hình thoi, hình chữ nhật, hình lục giác đều là những hình có trục đối xứng:

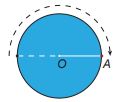
• Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn.
• Mỗi đường chéo là một trục đối xứng của hình thoi.
• Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
• Mỗi đường chéo, mỗi đường thẳng đi qua trung điểm hai cạnh đối diện của hình lục giác đều là một trục đối xứng của hình lục giác đều.

Lưu ý: Mỗi hình có thể có nhiều trục đối xứng.

3. HÌNH CÓ TÂM ĐỐI XỨNG TRONG THỰC TẾ

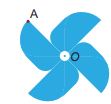
Hình tròn, hình chong chóng bốn cánh, khi quay nửa vòng quanh điểm O ta cũng được hình "chồng khít" với chính nó ở vị trí trước khi quay.

• Hình tròn, chong chóng hai cánh, chong chóng bốn cánh như nói ở trên đều có chung đặc điểm: Mỗi hình có một điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được "chồng khít" với chính nó ở vị trí ban đầu (trước khi quay).
• Những hình như thế gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Một số hình có tâm đối xứng trong thực tế

4. TÂM ĐỐI XỨNG CỦA MỘT SỐ HÌNH PHẲNG

Hình bình hành, hình lục giác đều, hình thoi, hình tròn, hình chữ nhật đều là các hình có tâm đối xứng:

• Tâm đối xứng của hình bình hành, hình thoi, hình chữ nhật là giao điểm của hai đường chéo.
• Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
• Tâm đối xứng của hình tròn là tâm của đường tròn đó.

Lưu ý. Có những hình có tâm đối xứng và có nhiều trục đối xứng. Cũng có hình không có tâm đối xứng như hình tam giác đều,..