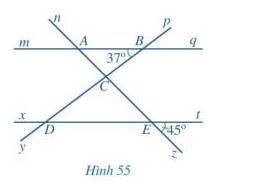
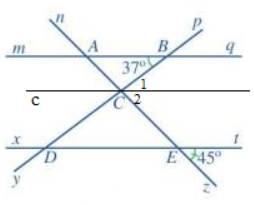
a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
a) Hai góc có tổng số đo bằng 180 \(^\circ \) có phải là hai góc kề bù hay không?
b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?
Thảo luận (1)Hướng dẫn giảia) Hai góc có tổng số đo bằng 180 \(^\circ \) không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng 180 \(^\circ \), chẳng hạn:
Góc xOy và góc xOz có tổng số đo bằng 180\(^\circ \) nhưng không phải là hai góc kề bù, vì không kề nhau
b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:
Góc mAq và nAp bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.
(Trả lời bởi Kiều Sơn Tùng)
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.
Thảo luận (1)Hướng dẫn giải
a) Vì \(\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên z // t
b) Vì \(\widehat {{D_1}}= \widehat {{C_1}} (= 90^\circ) \)
Mà 2 góc này ở vị trí đồng vị nên m // n
c) Vì \(\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \) ( 2 góc kề bù) nên \(110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ \)
Vì \(\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )\). Mà 2 góc này ở vị trí so le trong nên x // y
d) Vì \(\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ \)
Vì \(\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên u // v
(Trả lời bởi Hà Quang Minh)
Quan sát Hình 54, trong đó Cx song song với AB.
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.
Thảo luận (1)Hướng dẫn giảia) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)
(Trả lời bởi Hà Quang Minh)
Quan sát Hình 55, trong đó mq // xt
a) Kể tên các cặp góc đồng vị bằng nhau.
b) Tìm số đo các góc BAC, CDE.
c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được \(\widehat {BCE} = 82^\circ \). Theo em, bạn Nam nói đúng hay sai? Vì sao?
Thảo luận (1)Hướng dẫn giảia) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)
(Trả lời bởi Hà Quang Minh)
