Bài 7: Tứ giác nội tiếp

1. Khái niệm tứ giác nội tiếp

Một tứ giác có 4 đỉnh cùng nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

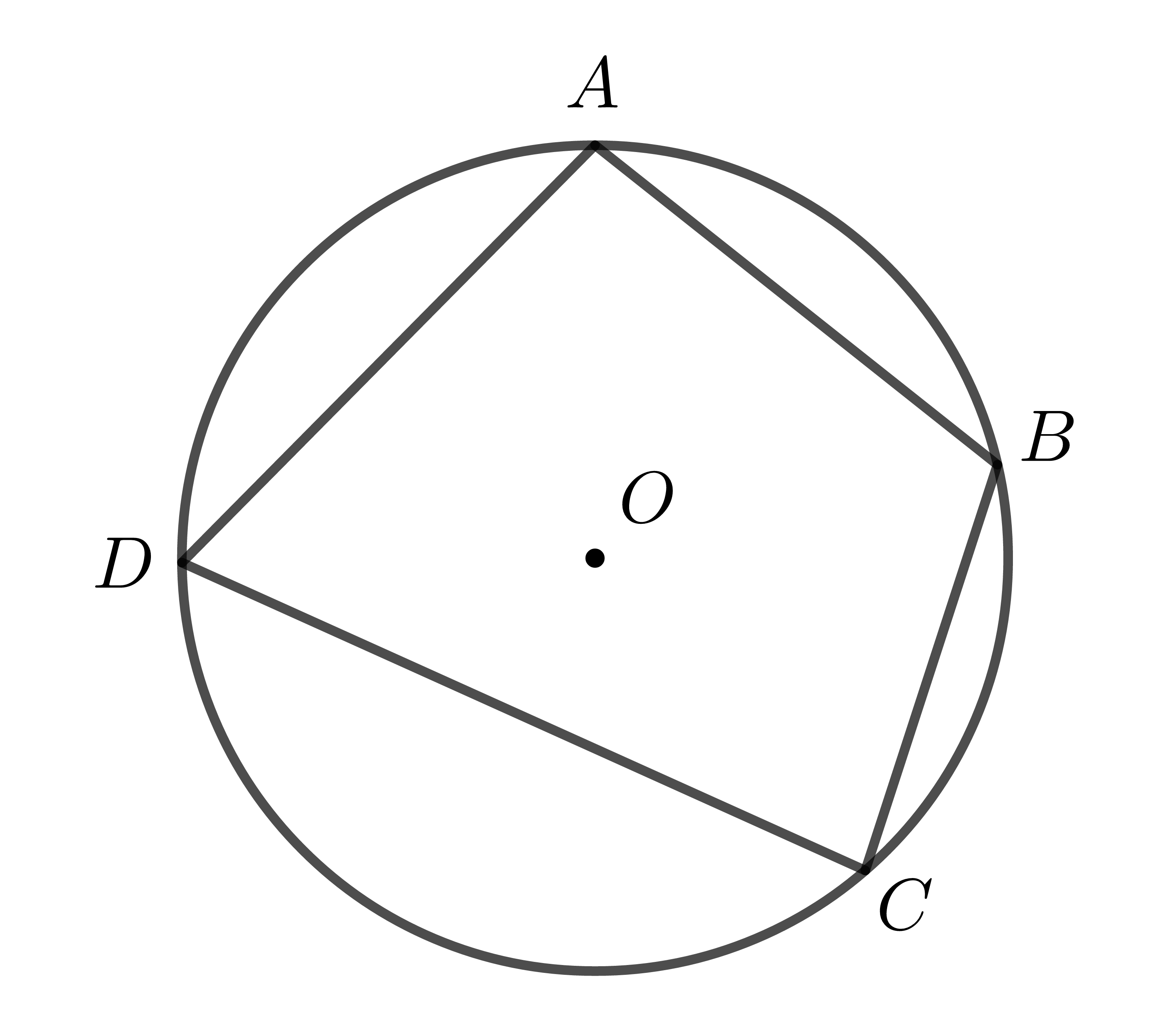
Tứ giác \(ABCD\) trong hình trên nội tiếp đường tròn \(\left(O\right)\).

Ví dụ: Các tứ giác dưới đây không là tứ giác nội tiếp:

2. Định lí

Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \(180^0\).

Cụ thể: Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left(O\right)\). Khi đó ta có:

\(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ADC}=180^0\\\widehat{BAC}+\widehat{BDC}=180^0\end{matrix}\right.\)

Ta dễ dàng chứng minh định lí trên như sau:

Ta có: \(\left\{{}\begin{matrix}\widehat{BAD}=\dfrac{1}{2}sđ\stackrel\frown{BAD}\\\widehat{BCD}=\dfrac{1}{2}sđ\stackrel\frown{BCD}\end{matrix}\right.\) (tính chất góc nội tiếp)

\(\Rightarrow\widehat{BAD}+\widehat{BCD}=\dfrac{1}{2}\left(sđ\stackrel\frown{BAD}+sđ\stackrel\frown{BCD}\right)=\dfrac{1}{2}.360^0=180^0\).

Hoàn toàn tương tự ta cũng có \(\widehat{ABC}+\widehat{ADC}=180^0\).

3. Định lí đảo

Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^0\) thì tứ giác đó nội tiếp đường tròn.

Chứng minh:

Giả sử tứ giác \(ABCD\) có \(\widehat{B}+\widehat{D}=180^0\).

Vẽ đường tròn tâm \(O\) đi qua 3 điểm \(A,B,C\) (ta luôn vẽ được đường tròn này vì 3 điểm \(A,B,C\) không thẳng hàng).

Hai điểm \(A\) và \(C\) chia đường tròn \(\left(O\right)\) thành hai cung \(\stackrel\frown{ABC},\stackrel\frown{AmC}\); trong đó cung \(AmC\) là cung chứa góc \(180^0-\widehat{B}\) dựng trên đoạn thẳng \(AC\).

Mặt khác: từ giả thiết suy ra \(\widehat{D}=180^0-\widehat{B}\)

\(\Rightarrow D\) nằm trên cung \(AmC\).

Vậy 4 điểm \(A,B,C,D\) cùng thuộc đường tròn \(\left(O\right)\) nên tứ giác \(ABCD\) là tứ giác nội tiếp.

Các dấu hiệu chứng minh một tứ giác là tứ giác nội tiếp:

• Tứ giác có tổng hai góc đối diện bằng \(180^0\).
• Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. 
• Tứ giác có 4 đỉnh cùng cách đều một điểm (ta có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
• Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha\).

Trên thực tế, dấu hiệu 1 và dấu hiệu 4 là hai dấu hiệu được sử dụng nhiều hơn cả.