Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.

I. VECTƠ TRONG KHÔNG GIAN

1. Định nghĩa và các phép toán

Cho đoạn thẳng \(AB\) trong không gian. Nếu ta chọn điểm đầu là \(A\), điểm cuối là \(B\) ta có một vectơ, kí hiệu là \(\overrightarrow{AB}\).

a) Định nghĩa

Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu \(\overrightarrow{AB}\) chỉ vectơ có điểm đầu là \(A\), điểm cuối là \(B\). Vectơ còn được kí hiệu là \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y}\),...

Các khái niệm liên qua như giá của vectơ, độ dài của vectơ, vectơ cùng phương, cùng hướng, vectơ - không, sự bằng nhau của hai vectơ,... được định nghĩa tương tự như trong mặt phẳng.

b) Phép cộng và phép trừ vectơ trong không gian

Phép cộng và phép trừ vectơ trong không gian được định nghĩa tương tự như phép cộng và phép trừ vectơ trong mặt phẳng. Phép cộng vectơ trong không gian cũng có những tính chất tương tự như phép cộng vectơ trong mặt phẳng. Ta vẫn có thể áp dụng các quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong mặt phẳng.

Quy tắc hình hộp:

Cho hình hộp \(ABCD.A'B'C'D'\) có ba cạnh xuất phát từ đỉnh \(A\) là \(AB,AD,AA'\) và có đường chéo là \(AC'\). Khi đó ta có quy tắc hình hộp là:

                     \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)

c) Phép nhân vectơ với một số

Trong không gian, tích của vectơ \(\overrightarrow{a}\) với một số \(k\ne0\) là vectơ \(k\overrightarrow{a}\) được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng.

2. Điều kiện đồng phẳng của ba vectơ

a) Khái niệm về sự đồng phẳng của ba vectơ

Trong không gian cho ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đều khác vectơ - không. Nếu từ một điểm \(O\) bất kì vẽ \(\overrightarrow{OA}=\overrightarrow{a}\), \(\overrightarrow{OB}=\overrightarrow{b}\), \(\overrightarrow{OC}=\overrightarrow{c}\) thì có thể xảy ra hai trường hợp:

+) Trường hợp các đường thẳng \(OA,OB,OC\) không cùng nằm trong một mặt phẳng, khi đó ta nói ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) không đồng phẳng.

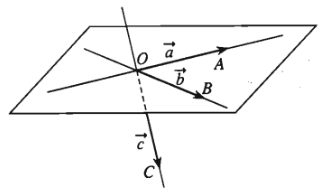
+) Trường hợp các đường thẳng \(OA,OB,OC\) cùng nằm trong một mặt phẳng thì ta nói ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đồng phẳng.

Trong trường hợp này giá của các vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) luôn song song với một mặt phẳng.

Chú ý: Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên không phụ thuộc vào việc chọn điểm \(O\).

b) Định nghĩa:

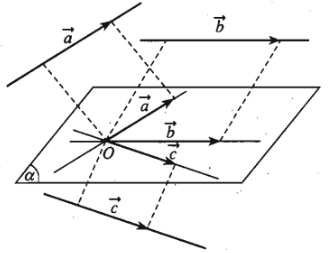
Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

c) Điều kiện để ba vectơ đồng phẳng

- Định lí 1: Trong không gian cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) không cùng phương và vectơ \(\overrightarrow{c}\). Khi đó ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đồng phẳng khi và chỉ khi có cặp số \(m,n\) sao cho \(\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\). Ngoài ra cặp số \(m,n\) là duy nhất.

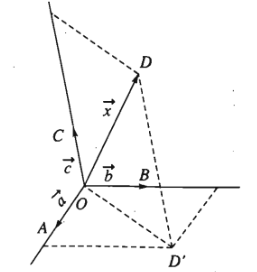
- Định lí 2: Trong không gian cho ba vectơ không đồng phẳng \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\). Khi đó với mọi vectơ \(\overrightarrow{x}\) ta đều tìm được một bộ ba số \(m,n,p\) sao cho \(\overrightarrow{x}=m\overrightarrow{a}+n\overrightarrow{b}+p\overrightarrow{c}\). Ngoài ra bộ ba số \(m,n,p\) là duy nhất.

II. HAI ĐƯỜNG THẲNG VUÔNG GÓC

1. Tích vô hướng của hai vectơ trong không gian

a) Góc giữa hai vectơ trong không gian

Định nghĩa: Trong không gian, cho \(\overrightarrow{u}\) và \(\overrightarrow{v}\) là hai vectơ khác vectơ - không. Lấy một điểm \(A\) bất kì, gọi \(B\) và \(C\) là hai điểm sao cho \(\overrightarrow{AB}=\overrightarrow{u}\), \(\overrightarrow{AC}=\overrightarrow{v}\). Khi đó ta gọi góc \(\widehat{BAC}\) (\(0^0\le\widehat{BAC}\le180^0\)) là góc giữa hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) trong không gian, kí hiệu là \(\left(\overrightarrow{u},\overrightarrow{v}\right)\).

b) Tích vô hướng của hai vectơ trong không gian

Định nghĩa:

Trong không gian cho hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) đều khác vectơ - không. Tích vô hướng của hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) là một số, kí hiệu là \(\overrightarrow{u}.\overrightarrow{v}\), được xác định bởi công thức:

                       \(\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.\cos\left(\overrightarrow{u},\overrightarrow{v}\right)\)

Trường hợp \(\overrightarrow{u}=\overrightarrow{0}\) hoặc \(\overrightarrow{v}=\overrightarrow{0}\) ta quy ước \(\overrightarrow{u}.\overrightarrow{v}=0\).

2. Vectơ chỉ phương của đường thẳng

a) Định nghĩa

Vectơ \(\overrightarrow{a}\) khác vectơ - không được gọi là vectơ chỉ phương của đường thẳng \(d\) nếu giá của vectơ \(\overrightarrow{a}\) song song hoặc trùng với đường thẳng \(d\).

b) Nhận xét

- Nếu \(\overrightarrow{a}\) là vectơ chỉ phương của đường thẳng \(d\) thì vectơ \(k\overrightarrow{a}\) với \(k\ne0\) cũng là vectơ chỉ phương của đường thẳng \(d\).

- Một đường thẳng \(d\) trong không gian hoàn toàn được xác định nếu biết một điểm \(A\) thuộc \(d\) là một vectơ chỉ phương \(\overrightarrow{a}\) của nó.

- Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.

3. Góc giữa hai đường thẳng trong không gian

a) Định nghĩa

Góc giữa hai đường thẳng \(a\) và \(b\) trong không gian là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song với \(a\) và \(b\).

b) Nhận xét

- Để xác định góc giữa hai đường thẳng \(a\) và \(b\) ta có thể lấy điểm \(O\) thuộc một trong hai đường thẳng đó rồi vec một đường thẳng qua \(O\) và song song với đường thẳng còn lại.

- Nếu \(\overrightarrow{u}\) là vectơ chỉ phương của đường thẳng \(a\) và \(\overrightarrow{v}\) là vectơ chỉ phương của đường thẳng \(b\) và \(\left(\overrightarrow{u},\overrightarrow{v}\right)=\alpha\) thì góc giữa hai đường thẳng \(a\) và \(b\) bằng \(\alpha\) nếu \(0^0\le\alpha\le90^0\) và bằng \(180^0-\alpha\) nếu \(90^0< \alpha\le180^0\). Nếu \(a\) và \(b\) song song hoặc trùng nhau thì góc giữa chúng bằng \(0^0\).

4. Hai đường thẳng vuông góc

a) Định nghĩa

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \(90^0\).

Kí hiệu: \(a\perp b,d\perp d',...\)

b) Nhận xét

- Nếu \(\overrightarrow{u}\) và \(\overrightarrow{v}\) lần lượt là các vectơ chỉ phương của hai đường thẳng \(a\) và \(b\) thì: \(a\perp b\Leftrightarrow\overrightarrow{u}.\overrightarrow{v}=0\).

- Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

- Hai đường thẳng vuông góc với nhau thì cắt nhau hoặc chéo nhau.

III. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

1. Định nghĩa

Đường thẳng \(d\) được gọi là vuông góc với mặt phẳng \(\left(\alpha\right)\) nếu \(d\) vuông góc với mọi đường thẳng \(a\) nằm trong mặt phẳng \(\left(\alpha\right)\).

Khi \(d\) vuông góc với \(\left(\alpha\right)\) ta còn nói \(\left(\alpha\right)\) vuông góc với \(d\), hoặc \(d\) và \(\left(\alpha\right)\) vuông góc với nhau và kí hiệu là \(d\perp\left(\alpha\right)\).

2. Điều kiện để đường thẳng vuông góc với mặt phẳng

Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.

3. Tính chất

Tính chất 1: Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Mặt phẳng trung trực của một đoạn thẳng:

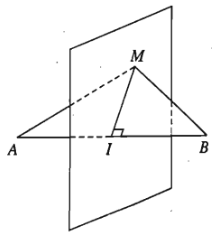
Người ta gọi mặt phẳng đi qua trung điểm \(I\) của đoạn thẳng \(AB\) và vuông góc với đường thẳng \(AB\) là mặt phẳng trung trực của đoạn thẳng \(AB\).

Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

4. Liên hệ giữa quan hệ song song và vuông góc

Tính chất 1:

a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

b) Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

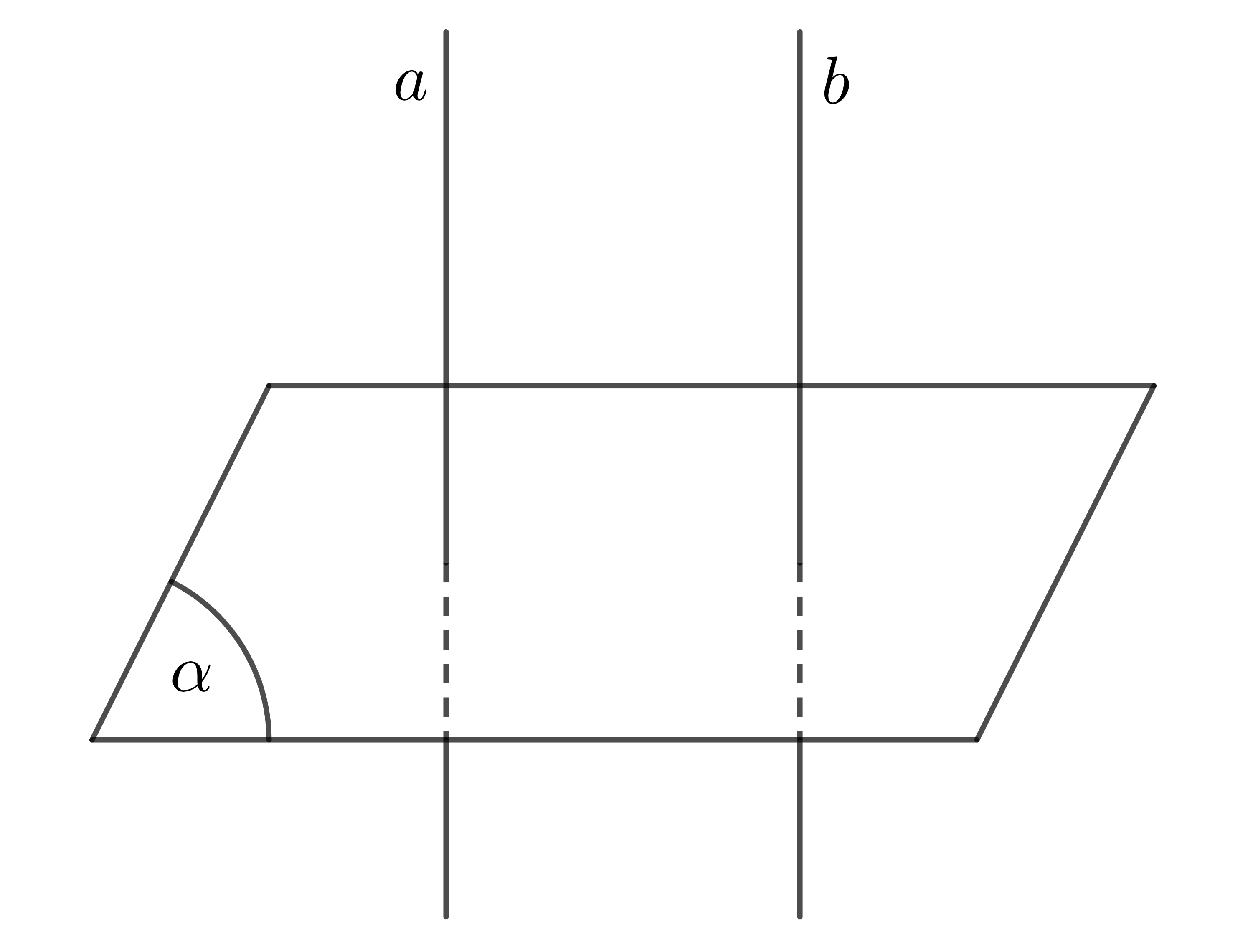
Tính chất 2: 

a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì hai mặt phẳng đó song song.

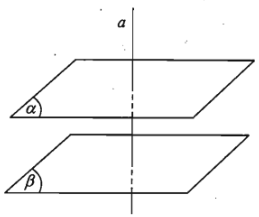
Tính chất 3:

a) Cho đường thẳng \(a\) và mặt phẳng \(\left(\alpha\right)\) song song với nhau. Đường thẳng nào vuông góc với \(\left(\alpha\right)\) thì cũng vuông góc với \(a\).

b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì song song với nhau.

5. Phép chiếu vuông góc và định lí ba đường vuông góc

a) Phép chiếu vuông góc

Cho đường thẳng \(\Delta\) vuông góc với mặt phẳng \(\left(\alpha\right)\). Phép chiếu song song theo phương của \(\Delta\) lên mặt phẳng \(\left(\alpha\right)\) được gọi phép chiếu vuông góc lên mặt phẳng \(\left(\alpha\right)\).

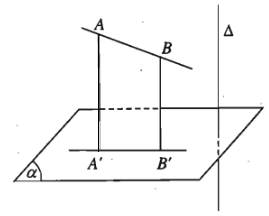
b) Định lí ba đường thẳng vuông góc

Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left(\alpha\right)\) và \(b\) là đường thẳng không thuộc \(\left(\alpha\right)\) đồng thời không vuông góc với \(\left(\alpha\right)\). Gọi \(b'\) là hình chiếu vuông góc của \(b\) lên \(\left(\alpha\right)\). Khi đó \(a\) vuông góc với \(b\) khi và chỉ khi \(a\) vuông góc với \(b'\).

c) Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\). 

Trường hợp đường thẳng \(d\) vuông góc với mặt phẳng \(\left(\alpha\right)\) thì ta nói góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\)  bằng \(90^0\).

Trường hợp đường thẳng \(d\) không vuông góc với mặt phẳng \(\left(\alpha\right)\) thì góc giữa \(d\) và hình chiếu \(d'\) của nó trên \(\left(\alpha\right)\) được gọi là góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\). 

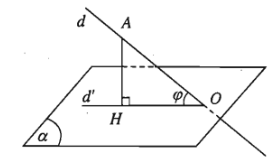
Chú ý: Nếu \(\varphi\) là góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\) thì ta luôn có \(0^0\le\varphi\le90^0\).

IV. HAI MẶT PHẲNG VUÔNG GÓC

1. Góc giữa hai mặt phẳng

a) Định nghĩa

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

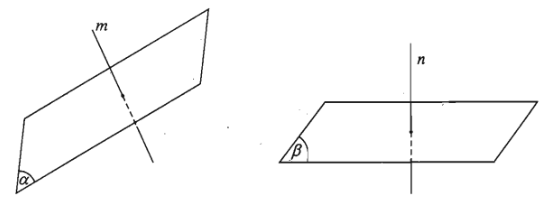
Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói góc giữa hai mặt phẳng đó bằng \(0^0\).

b) Cách xác định góc giữa hai mặt phẳng cắt nhau

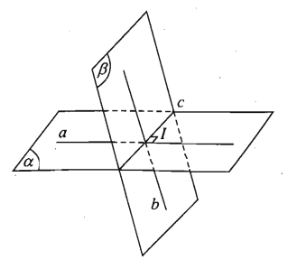
Giả sử hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) cắt nhau theo giao tuyến \(c\). Từ một điểm \(I\) bất kì trên \(c\) ta dựng trong \(\left(\alpha\right)\) một đường thẳng \(a\) vuông góc với \(c\) và dựng trong \(\left(\beta\right)\) một đường thẳng \(b\) vuông góc với \(c\).

Góc giữa hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) là góc giữa hai đường thẳng \(a\) và \(b\).

c) Diện tích hình chiếu của một đa giác

Cho đa giác \(H\) nằm trong mặt phẳng \(\left(\alpha\right)\) có diện tích \(S\) và \(H'\) là hình chiếu vuông góc của \(H\) trên mặt phẳng \(\left(\beta\right)\). Khi đó diện tích \(S'\) của \(H'\) được tính theo công thức:

                                       \(S'=S\cos\varphi\)

với \(\varphi\) là góc giữa \(\left(\alpha\right)\) và \(\left(\beta\right)\).

2. Hai mặt phẳng vuông góc

a) Định nghĩa

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông.

Nếu hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) vuông góc với nhau ta kí hiệu là \(\left(\alpha\right)\perp\left(\beta\right)\).

b) Các định lí

- Định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

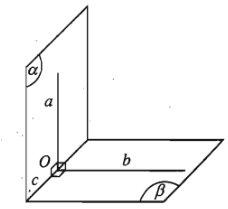
Hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với đường thẳng kia.

Hệ quả 2: Cho hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng \(\left(\alpha\right)\) ta dựng một đường thẳng vuông góc với mặt phẳng \(\left(\beta\right)\) thì đường thẳng này nằm triong mp \(\left(\alpha\right)\).

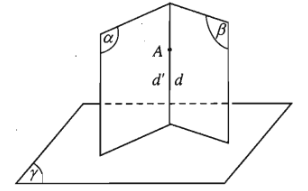
- Định lí 2: Nếu hai mặt phẳng vuông góc nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

V. KHOẢNG CÁCH

1. Khoảng cách từ một điểm đến một đường thẳng

Cho điểm \(O\) và đường thẳng \(a\). Trong mặt phẳng \(\left(O,a\right)\) gọi \(H\) là hình chiếu vuông góc của \(O\) trên \(a\). Khi đó khoảng cách giữa hai điểm \(O\) và \(H\) được gọi là khoảng cách từ điểm \(O\) đến đường thẳng \(a\), kí hiệu là \(d\left(O,a\right)\).

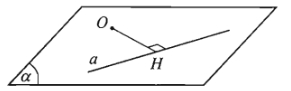
2. Khoảng cách từ một điểm đến một mặt phẳng

Cho điểm \(O\) và mặt phẳng \(\left(\alpha\right)\). Gọi \(H\) là hình chiếu vuông góc của \(O\) lên mặt phẳng \(\left(\alpha\right)\). Khi đó khoảng cách giữa hai điểm \(O\) và \(H\) được gọi là khoảng cách từ điểm \(O\) đến mặt phẳng \(\left(\alpha\right)\), kí hiệu là \(d\left(O;\left(\alpha\right)\right)\).

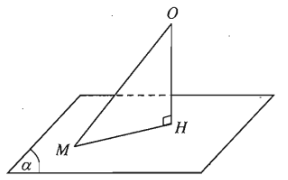
3. Khoảng cách giữa đường thẳng và mặt phẳng song song

Cho đường thẳng \(a\) song song với mặt phẳng \(\left(\alpha\right)\). Khoảng cách giữa đường thẳng \(a\) và mặt phẳng \(\left(\alpha\right)\) là khoảng cách từ một điểm bất kì của \(a\) đến mặt phẳng \(\left(\alpha\right)\), kí hiệu là \(d\left(a,\left(\alpha\right)\right)\).

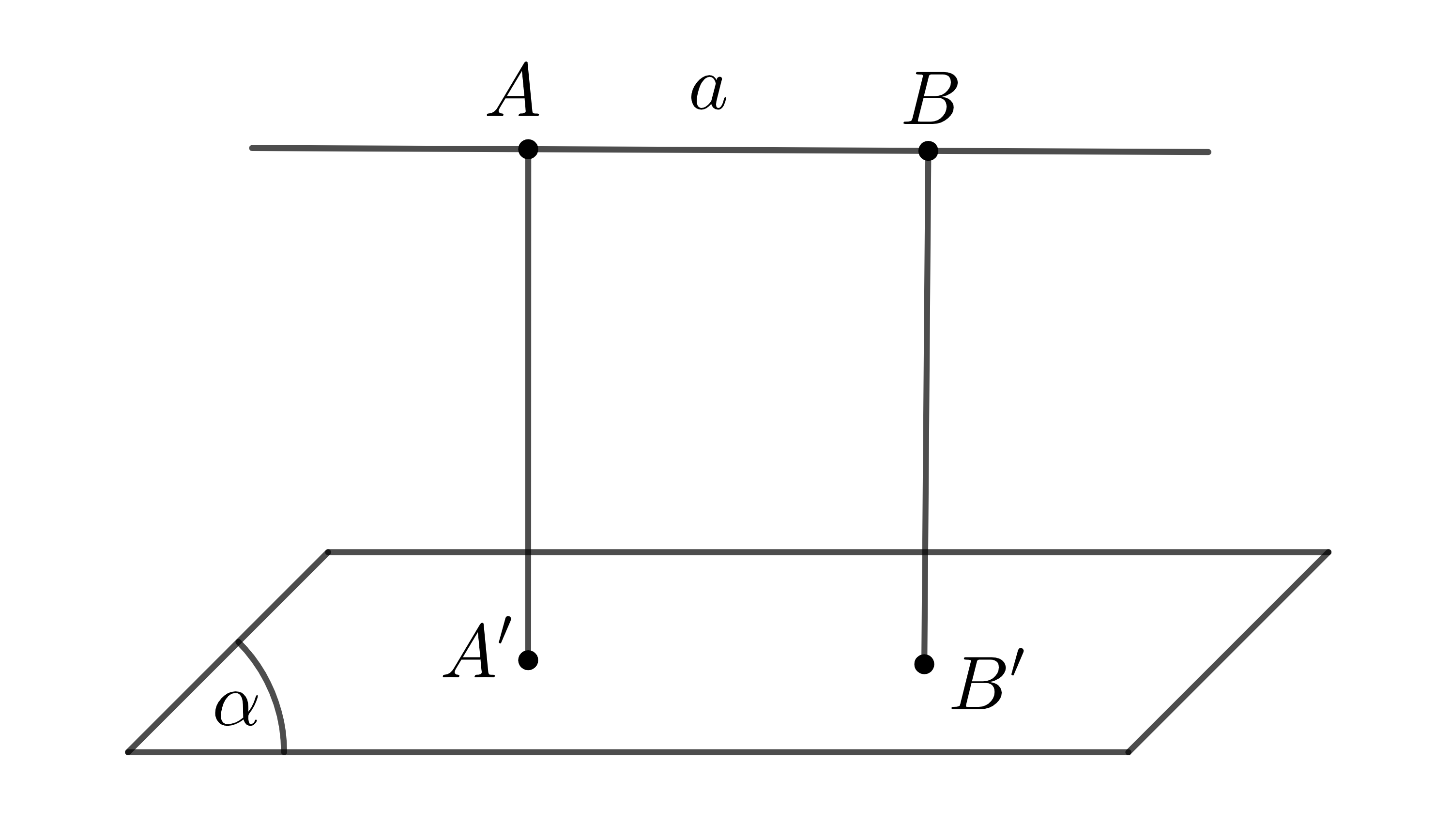
4. Khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

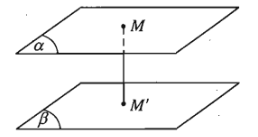
Ta kí hiệu khoảng cách giữa hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) song song với nhau là \(d\left(\left(\alpha\right),\left(\beta\right)\right)\). Khi đó \(d\left(\left(\alpha\right),\left(\beta\right)\right)=d\left(M,\left(\beta\right)\right)\) với \(M\in\left(\alpha\right)\), và \(d\left(\left(\alpha\right),\left(\beta\right)\right)=d\left(M',\left(\alpha\right)\right)\) với \(M'\in\left(\beta\right)\).

5. Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau

a) Định nghĩa

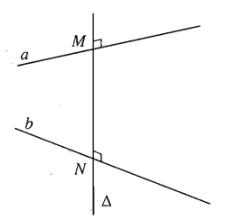
- Đường thẳng \(\Delta\) cắt hai đường thẳng chéo nhau \(a\) và \(b\) và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của \(a\) và \(b\).

- Nếu đường thẳng vuông góc chung \(\Delta\) cắt hai đường thẳng chéo nhau \(a\), \(b\) lần lượt tại \(M,N\) thì độ dài đoạn thẳng \(MN\) gọi là khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\).

b) Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau

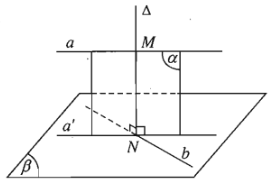
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Gọi \(\left(\beta\right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(a'\) là hình chiếu vuông góc của \(a\) trên mặt phẳng \(\left(\beta\right)\).

Gọi \(N\) là giao điểm của \(a'\) và \(b\). Gọi \(\left(\alpha\right)\) là mp chứa \(a\) và \(a'\), \(\Delta\) là đường thẳng đi qua \(N\) và vuông góc với \(\left(\beta\right)\). Như vậy \(\Delta\) cắt \(a\) tại \(M\) và cắt \(b\) tại \(N\), đồng thời \(\Delta\) vuông góc với cả \(a\) và \(b\). Do đó \(\Delta\) là đường vuông góc chung của \(a\) và \(b\).

c) Nhận xét

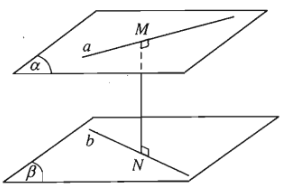
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.

- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.