Bài 6: Ôn tập chương Đường thẳng và mặt phẳng trong không gian. Quan hệ song song.

I. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Mặt phẳng

Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.

Để kí hiệu mặt phẳng, ta thường dùng chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ngoặc ( ).

Ví dụ: mặt phẳng \(\left(P\right)\), mặt phẳng \(\left(Q\right)\), mặt phẳng \(\left(\alpha\right)\), mặt phẳng \(\left(\beta\right)\) hoặc viết tắt là \(mp\left(P\right)\), \(mp\left(Q\right)\), \(mp\left(\alpha\right)\), \(mp\left(\beta\right)\) hoặc \(\left(P\right)\), \(\left(Q\right)\), \(\left(\alpha\right)\), \(\left(\beta\right)\),...

2. Điểm thuộc mặt phẳng

Cho điểm \(A\) và mặt phẳng \(\left(\alpha\right)\).

Khi điểm \(A\) thuộc mặt phẳng \(\left(\alpha\right)\) ta nói \(A\) nằm trên \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) chứa \(A\), hay \(\left(\alpha\right)\) đi qua \(A\) và được kí hiệu là \(A\in\left(\alpha\right)\).

Khi điểm \(A\) không thuộc mặt phẳng \(\left(\alpha\right)\) ta nói điểm \(A\) nằm ngoài \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) không chứa \(A\) và được kí hiệu là \(A\notin\left(\alpha\right)\).

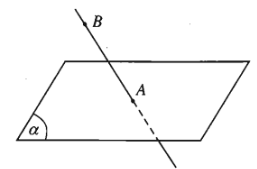
Ví dụ: Trong hình vẽ dưới đây, \(A\in\left(\alpha\right)\) còn \(B\notin\left(\alpha\right)\):

3. Hình biểu diễn của một hình không gian

Để vẽ hình biểu diễn của một hình không gian, ta dựa vào các quy tắc sau:

- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.

- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.

- Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.

4. Các tính chất

Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Như vậy một mặt phẳng hoàn toàn xác định nếu biết nó đi qua ba điểm không thẳng hàng. Ta kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng \(A,B,C\) là mặt phẳng \(\left(ABC\right)\) hoặc \(mp\left(ABC\right)\) hoặc \(\left(ABC\right)\).

Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt cùng thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Nếu mọi điểm của đường thẳng \(d\) đều thuộc mặt phẳng \(\left(\alpha\right)\) thì ta nói đường thẳng \(d\) nằm trong \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) chứa \(d\) và kí hiệu là \(d\subset\left(\alpha\right)\) hay \(\left(\alpha\right)\supset d\).

Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói rằng chúng không đồng phẳng.

Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.

Đường thẳng \(d\) chung của hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) được gọi là giao tuyến của \(\left(\alpha\right)\) và \(\left(\beta\right)\) và kí hiệu là \(d=\left(\alpha\right)\cap\left(\beta\right)\).

Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

5. Cách xác định một mặt phẳng

Ba cách xác định mặt phẳng

a) Mặt phẳng được hoàn toàn xác định nếu biết nó đi qua ba điểm không thẳng hàng.

b) Mặt phẳng được hoàn toàn xác định nếu biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

Cho đường thẳng \(d\) và điểm \(A\notin d\). Khi đó điểm \(A\) và đường thẳng \(d\) xác định một mặt phẳng, kí hiệu là \(mp\left(A,d\right)\) hay \(mp\left(d,A\right)\) hay \(\left(d,A\right)\).

c) Mặt phẳng được hoàn toàn xác định nếu biết nó chứa hai đường thẳng cắt nhau.

Cho hai đường thẳng cắt nhau \(a\) và \(b\). Khi đó hai đường thẳng \(a\) và \(b\) xác định một mặt phẳng, kí hiệu là \(mp\left(a,b\right)\) hay \(\left(a,b\right)\), hoặc \(mp\left(b,a\right)\) hay \(\left(b,a\right)\).

6. Hình chóp. Hình tứ diện.

1. Trong mặt phẳng \(\left(\alpha\right)\), cho đa giác lồi \(A_1A_2...A_n\). Lấy điểm \(S\) nằm ngoài \(\left(\alpha\right)\). Lần lượt nối \(S\) với các điểm \(A_1,A_2,...,A_n\) ta được \(n\) tam giác \(SA_1A_2\), \(SA_2A_3\),..., \(SA_nA_1\). Hình gồm đa giác \(A_1A_2...A_n\) và \(n\) tam giác \(SA_1A_2\), \(SA_2A_3\),..., \(SA_nA_1\) gọi là hình chóp, kí hiệu là \(S.A_1A_2...A_n\).

Ta gọi \(S\) là đỉnh; đa giác \(A_1A_2...A_n\) là mặt đáy; các tam giác \(SA_1A_2\), \(SA_2A_3\), ..., \(SA_nA_1\) là các mặt bên; các đoạn \(SA_1,SA_2,...SA_n\) là các cạnh bên; các cạnh của đa giác đáy là các cạnh đáy. 

Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,... lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,...

2. Cho bốn điểm không đồng phẳng \(A,B,C,D\). HÌnh gồm bốn tam giác \(ABC,ABD,ACD,BCD\) gọi là hình tứ diện (hay gọi ngắn là tứ diện) và được kí hiệu là \(ABCD\). Các điểm \(A,B,C,D\) gọi là các đỉnh của tứ diện. Các đoạn \(AB,BC,CD,DA\) là các cạnh của tứ diện, Hai cạnh không đi qua một điểm gọi là hai cạnh đối diện. Các tam giác \(ABC,ABD,ACD,BCD\) gọi là các mặt của tứ diện. Đỉnh không nằm trên một mặt của tứ diện gọi là đỉnh đối diện với mặt đó.

Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.

Chú ý:

+) Khi nói đến đa giác ta có thể hiểu là tập hợp các điểm thuộc các cạnh của đa giác và các điểm trong đa giác đó.

+) Thiết diện hay mặt cắt của hình \(\left(H\right)\) khi cắt bởi mp\(\left(\alpha\right)\) là phần chung của \(\left(H\right)\) và \(\left(\alpha\right)\).

II. HAI ĐƯỜNG CHÉO NHAU VÀ HAI ĐƯỜNG SONG SONG

1. Vị trí tương đối của hai đường thẳng trong không gian

Cho hai đường thẳng \(a\) và \(b\) trong không gian. Có thể xảy ra một trong hai trường hợp:

Trường hợp 1: Có một mặt phẳng chứa \(a\) và \(b\).

Khi đó ta nói \(a\) và \(b\) đồng phẳng. Có ba khả năng xảy ra:

+) \(a\) và \(b\) có điểm chung duy nhất là \(M\), ta nói \(a\) và \(b\) cắt nhau tại \(M\), kí hiệu là \(a\cap b=\left\{M\right\}\) hoặc có thể viết \(a\cap b=M\).

+) \(a\) và \(b\) không có điểm chung. Ta nói  \(a\) và \(b\) song song với nhau và kia hiệu là  \(a\) // \(b\) .

+) \(a\) trùng \(b\), kí hiệu \(a\equiv b\).

Như vậy, hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.

Trường hợp 2: Không có mặt phẳng nào chứa \(a\) và \(b\).

Khi đó ta nói  \(a\) và \(b\) chéo nhau hay \(a\) chéo với \(b\):

2. Tính chất

- Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

Nhận xét: Hai đường thẳng song song \(a\) và \(b\) xác định một mặt phẳng, kí hiệu là \(mp\left(a,b\right)\) hay \(\left(a,b\right)\).

- Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc là đồng quy hoặc là đôi một song song với nhau.

Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng hoặc trùng với một trong hai đường thẳng đó.

- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

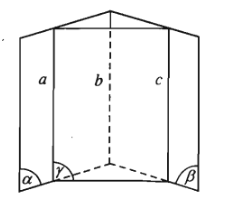
Ta gọi chúng là ba đường thẳng song song.

III. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

1. Vị trí tương đối của đường thẳng và mặt phẳng

Cho đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\). Tuỳ theo số điẻm chung của \(d\) và \(\left(\alpha\right)\) ta có 3 trường hợp sau:

+) \(d\) và \(\left(\alpha\right)\) không có điểm chung. Khi đó ta nói  \(d\) song song với \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) song song với  \(d\) và kí hiệu là  \(d\)//\(\left(\alpha\right)\) hay \(\left(\alpha\right)\)//\(d\).

+) \(d\) và \(\left(\alpha\right)\) có một điểm chung duy nhất \(M\). Khi đó ta nói  \(d\) và \(\left(\alpha\right)\) cắt nhau tại điểm \(M\) và kí hiệu là \(d\cap\left(\alpha\right)=\left\{M\right\}\) hay \(d\cap\left(\alpha\right)=M\).

+) \(d\) và \(\left(\alpha\right)\) có từ hai điểm chung trở lên. Khi đó \(d\) nằm trong \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) chứa \(d\) và kí hiệu là \(d\subset\left(\alpha\right)\) hay \(\left(\alpha\right)\supset d\).

2. Tính chất

- Nếu đường thẳng \(d\) không nằm trong mặt phẳng \(\left(\alpha\right)\) và \(d\) song song với đường thẳng \(d'\) nằm trong \(\left(\alpha\right)\) thì \(d\) song song với \(\left(\alpha\right)\).

- Cho đường thẳng \(a\) song song với mặt phẳng \(\left(\alpha\right)\). Nếu mặt phẳng \(\left(\beta\right)\) chứa \(a\) và cắt \(\left(\alpha\right)\) theo giao tuyến \(b\) thì \(b\) song song với \(a\).

- Nếu hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Hai đường thẳng chéo nhau thì không thể nằm trong cùng một mặt phẳng. Tuy nhiên ta có thể tìm được mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

- Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

IV. HAI MẶT PHẲNG SONG SONG

1. Định nghĩa

Hai mặt phẳng \(\left(\alpha\right)\), \(\left(\beta\right)\) được gọi là song song với nhau nếu chúng không có điểm chung.

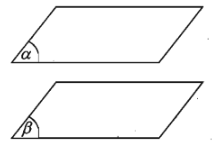
Khi đó ta kí hiệu: \(\left(\alpha\right)\)//\(\left(\beta\right)\) hay \(\left(\beta\right)\)//\(\left(\alpha\right)\).

2. Tính chất

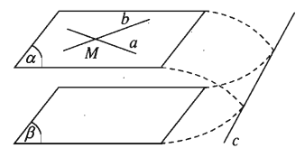
- Nếu mặt phẳng \(\left(\alpha\right)\) chứa hai đường thẳng cắt nhau \(a,b\) và \(a,b\) cùng song song với mặt phẳng \(\left(\beta\right)\) thì \(\left(\alpha\right)\) song song với \(\left(\beta\right)\).

- Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

Từ định lí trên ta suy ra các hệ quả sau:

+) Nếu đường thẳng \(d\) song song với mặt phẳng \(\left(\alpha\right)\) thì qua \(d\) có duy nhất một mặt phẳng song song với \(\left(\alpha\right)\).

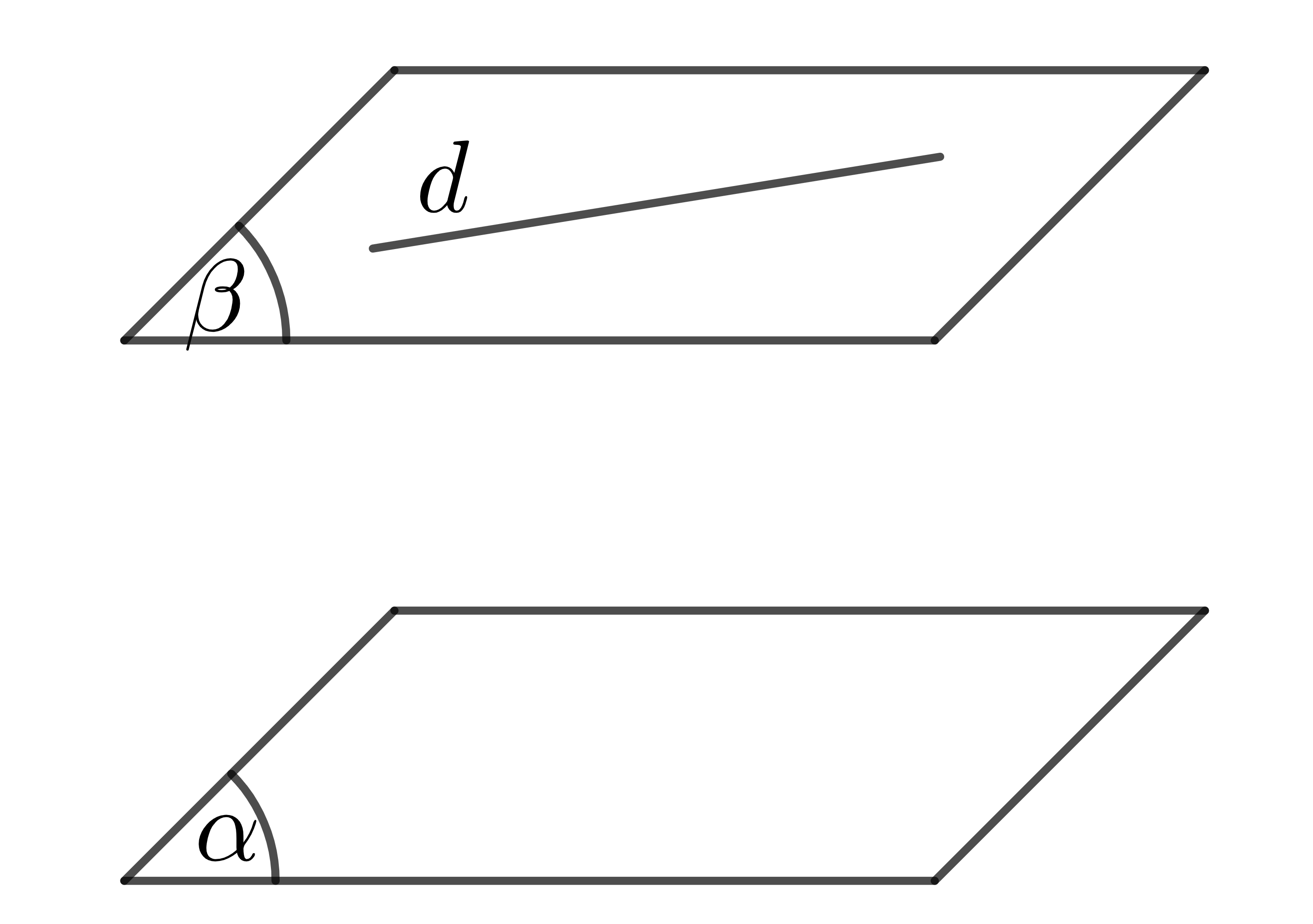
+) Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

+) Cho điểm \(A\) không nằm trên mặt phẳng \(\left(\alpha\right)\). Mọi đường thẳng đi qua \(A\) và song song với \(\left(\alpha\right)\) đều nằm trong mặt phẳng đi qua \(A\) và song song với \(\left(\alpha\right)\).

- Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

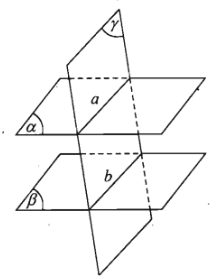
Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.

3. Định lí Ta-lét

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

Nếu \(d,d'\) là hai cát tuyến bất kì cắt ba mặt phẳng song song \(\left(\alpha\right)\), \(\left(\beta\right)\), \(\left(\gamma\right)\) lần lượt tại các điểm \(A,B,C\) và \(A',B',C'\) thì \(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{CA}{C'A'}\).

4. Hình lăng trụ và hình hộp

Nhận xét:

+) Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.

+) Các mặt bên của hình lăng trụ là các hình bình hành.

+) Hai đáy của hình lăng trụ là hai đa giác bằng nhau.

Người ta gọi tên của hình lăng trụ dựa vào tên của đa giác đáy:

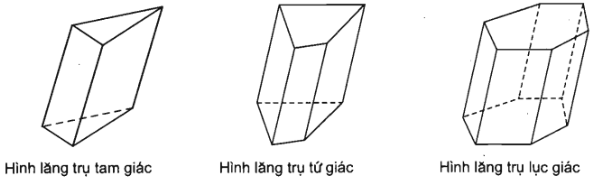
Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.

5. Hình chóp cụt

Cho hình chóp \(S.A_1A_2...A_n\), một mặt phẳng \(\left(P\right)\) không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh \(SA_1,SA_2,...SA_n\) lần lượt tại \(A'_1,A'_2,...,A'_n\). HÌnh tạo bởi thiết diện \(A'_1A'_2...A'_n\) và đáy \(A_1A_2...A_n\) của hình chóp cùng với các tứ giác \(A'_1A'_2A_2A_1\), \(A'_2A'_3A_3A_2\), ..., \(A'_nA'_1A_1A_n\) được gọi là hình chóp cụt.

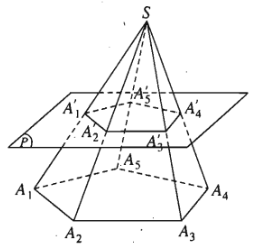
 Tuỳ theo đáy là tam giác, tứ giác, ngũ giác,... ta có hình chóp  cụt tam giác, hình chóp cụt tứ giác, hình chóp cụt ngũ giác,...

Tính chất:

1) Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.

2) Các mặt bên là các hình thang.

3) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

V. PHÉP CHIẾU SONG SONG

1. Phép chiếu song song

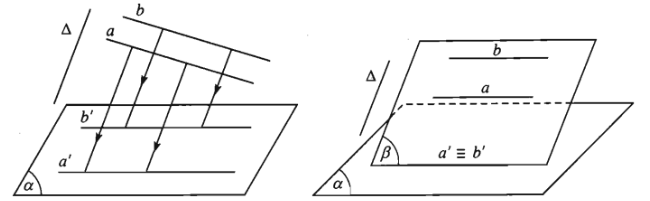
Cho mặt phẳng \(\left(\alpha\right)\) và đường thẳng \(\Delta\) cắt \(\left(\alpha\right)\).

Với mỗi điểm \(M\) trong không gian, đường thẳng đi qua \(M\) và song song hoặc trùng với \(\Delta\) sẽ cắt \(\left(\alpha\right)\) tại điểm \(M'\) xác định. Điểm \(M'\) được gọi là hình chiếu song song của điểm \(M\) trên mặt phẳng \(\left(\alpha\right)\) theo phương của đường thẳng \(\Delta\) hoặc nói gọn là theo phương \(\Delta\).

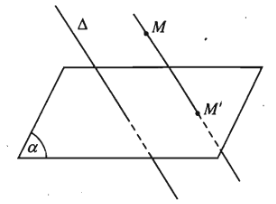
Mặt phẳng \(\left(\alpha\right)\) được gọi là mặt phẳng chiếu. Phương \(\Delta\) gọi là phương chiếu.

Phép đặt tương ứng mỗi điểm \(M\) trong không gian với hình chiếu \(M'\) của nó trên mặt phẳng \(\left(\alpha\right)\) được gọi là phép chiếu song song lên \(\left(\alpha\right)\) theo phương \(\Delta\).

Nếu \(H\) là một hình nào đó thì tập hợp \(H'\) các hình chiếu \(M'\) của tất cả những điểm \(M\) thuộc \(H\) được gọi là hình chiếu của \(H\) qua phép chiếu song song nói trên.

Chú ý: Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó là một điểm. 

2. Các tính chất của phép chiếu song song

a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

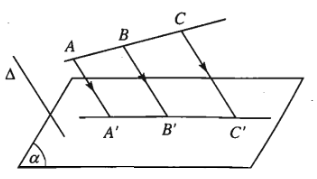
b) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

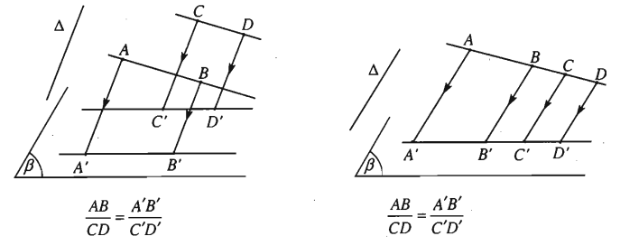
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

3. Hình biểu diễn của một hình không gian trên mặt phẳng

Hình biểu diễn của các hình thường gặp:

Tam giác: Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tuỳ ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông,...)

Hình bình hành: Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tuỳ ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật,...)

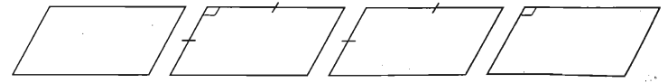
Hình thang: Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tuỳ ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.

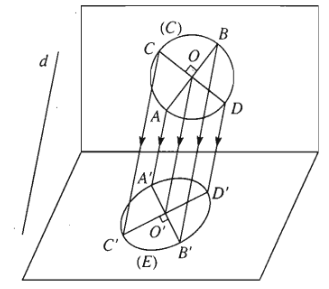
Hình tròn: Người ta thường đùng elip để biểu diễn cho hình tròn.