Bài 4: Ôn tập chương nguyên hàm, tích phân và ứng dụng
Nội dung lý thuyết
Các phiên bản khácI. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số \(f\left(x\right)\) xác định trên tập \(K\). Hàm số \(F\left(x\right)\) gọi là nguyên hàm của \(f\left(x\right)\) trên \(K\) nếu \(F'\left(x\right)=f\left(x\right)\) với mọi \(x\in K\).
Ví dụ: Hàm \(F\left(x\right)=x^2\) là nguyên hàm của hàm \(f\left(x\right)=2x\) trên tập số thực \(R\), vì \(F'\left(x\right)=\left(x^2\right)'=2x=f\left(x\right),\forall x\in R\) ;
- Định lí 1: Nếu \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(K\) thì với mỗi hằng số \(C\), hàm số \(G\left(x\right)=F\left(x\right)+C\) cũng là một nguyên hàm của \(f\left(x\right)\) trên \(K\).
- Định lí 2: Nếu \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(K\) thì mọi nguyên hàm của \(f\left(x\right)\) trên \(K\) đều có dạng \(F\left(x\right)+C\), với \(C\) là một hằng số.
Từ hai định lí trên cho thấy:
Nếu \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(K\) thì \(F\left(x\right)+C\), \(C\in R\) là họ tất cả nguyên hàm của \(f\left(x\right)\) trên \(K\). Kí hiệu: \(\int f\left(x\right)dx=F\left(x\right)+C\)
Chú ý: Biểu thức \(f\left(x\right)dx\) chính là vi phân của nguyên hàm \(F\left(x\right)\) của \(f\left(x\right)\), vì \(\text{d}F\left(x\right)=F'\left(x\right)\text{ }dx=f\left(x\right)\text{ }dx\).
Ví dụ: +) Với \(x\in R\), \(\int2xdx=x^2+C\) ;
+) Với \(s\in\left(0;+\infty\right)\), \(\int\dfrac{1}{s}ds=\ln s+C\).
2. Tính chất của nguyên hàm
- Tính chất 1: \(\int f'\left(x\right)\text{dx}=f\left(x\right)+C\)
Ví dụ: \(\int\left(\cos x\right)'\text{ }dx=\int\left(-\sin x\right)\text{ }dx=\cos x+C\)
- Tính chất 2: \(\int k.f\left(x\right)\text{ }dx=k\int f\left(x\right)\text{ }dx\) (với \(k\) là một hằng số khác 0).
- Tính chất 3: \(\int\left[f\left(x\right)\pm g\left(x\right)\right]\text{ }dx=\int f\left(x\right)\text{ }dx\pm\int g\left(x\right)\text{ }dx\).
3. Sự tồn tại nguyên hàm
- Định lí 3: Mọi hàm số \(f\left(x\right)\) mà liên tục trên \(K\) đều có nguyên hàm trên \(K\).
Ví dụ: Hàm số \(f\left(x\right)=x^{\dfrac{2}{3}}\) có nguyên hàm trên khoảng \(\left(0;+\infty\right)\) và \(\int x^{\dfrac{2}{3}}dx=\dfrac{3}{5}x^{\dfrac{5}{3}}+C\)
4. Bảng nguyên hàm của một số hàm thường gặp
| \(\int0dx=C\) | \(\int a^xdx=\dfrac{a^x}{\ln a}+C\left(a>0,a\ne1\right)\) |
| \(\int dx=x+C\) | \(\int\cos xdx=\sin x+C\) |
| \(\int x^{\alpha}dx=\dfrac{1}{\alpha+1}x^{\alpha+1}+C\left(\alpha\ne-1\right)\) | \(\int\sin xdx=-\cos x+C\) |
| \(\int\dfrac{1}{x}dx=\ln\left|x\right|+C\) | \(\int\dfrac{1}{\cos^2x}dx=\tan x+C\) |
| \(\int e^xdx=e^x+C\) | \(\int\dfrac{1}{\sin^2x}dx=-\cot x+C\) |
5. Phương pháp tính nguyên hàm
a) Phương pháp đổi biến số
Định lí: Nếu \(\int f\left(u\right)du=F\left(u\right)+C\) và \(u=u\left(x\right)\) là hàm số có đạo hàm liên tục thì
\(\int f\left(u\left(x\right)\right)u'\left(x\right)dx=F\left(u\left(x\right)\right)+C\).
Hệ quả: Với \(u=ax+b\left(a\ne0\right)\) ta có
\(\int\left(ax+b\right)dx=\dfrac{1}{a}F\left(ax+b\right)+C\)
Ví dụ: Vì \(\int\sin udu=-\cos u+C\) nên theo hệ quả ta có \(\int\sin\left(3x-1\right)dx=-\dfrac{1}{3}\cos\left(3x-1\right)+C\)
b) Phương pháp tính nguyên hàm từng phần
Nếu hai hàm số \(u=u\left(x\right)\) và \(v=v\left(x\right)\) có đạo hàm liên tục trên \(K\) thì
\(\int u\left(x\right)v'\left(x\right)dx=u\left(x\right)v\left(x\right)-\int u'\left(x\right)v\left(x\right)dx\).
Chú ý: Vì \(v'\left(x\right)dx=dv\), \(u'\left(x\right)dx=du\) nên ta có thể viết thành
\(\int udv=uv-\int vdu\).
Ví dụ: Tính \(\int xe^xdx\).
Giải:
Đặt \(u=x\) và \(dv=e^xdx\) ta có \(du=dx\) và \(v=e^x\)
Do đó \(\int xe^xdx=xe^x-\int e^xdx=xe^x-e^x+C\)
@75837@
II. TÍCH PHÂN
1. Khái niệm tích phân
Cho \(f\left(x\right)\) là hàm số liên tục trên đoạn \(\left[a;b\right]\). Giả sử \(F\left(x\right)\) là một nguyên hàm của \(f\left(x\right)\) trên đoạn \(\left[a;b\right]\). Hiệu số \(F\left(b\right)-F\left(a\right)\) được gọi là tích phân từ \(a\) đến \(b\) (hay tích phân xác định trên đoạn \(\left[a;b\right]\)) của hàm số \(f\left(x\right)\), kí hiệu là: \(\int_a^bf\left(x\right)dx\).
Ta còn dùng kí hiệu \(F\left(x\right)|^b_a\) để chỉ hiệu số \(F\left(b\right)-F\left(a\right)\).
Vậy \(\int_a^bf\left(x\right)\text{dx}=F\left(x\right)|^b_a=F\left(b\right)-F\left(a\right)\)
Ta gọi \(\int\limits^b_a\) là dấu tích phân, a là cận dưới, b là cận trên, \(f\left(x\right)dx\) là biểu thức dưới dấu tích phân và \(f\left(x\right)\) là hàm số dưới dấu tích phân.
Chú ý: Trong trường hợp \(a=b\) hoặc \(a>b\), ta có quy ước:
\(\int_a^af\left(x\right)dx=0;\int_a^bf\left(x\right)dx=-\int_b^af\left(x\right)dx\)
Ví dụ:
+) \(\int_1^22xdx=x^2|^2_1=2^2-1^2=4-1=3\) ;
+) \(\int_1^e\dfrac{1}{t}\text{dt}=\ln t|^e_1=\ln e-\ln1=1-0=1\).
Nhận xét:
a) Tích phân của hàm số \(f\) từ \(a\) đến \(b\) có thể kí hiệu bởi \(\int_a^bf\left(x\right)dx\) hay \(\int_a^bf\left(t\right)dt\). Tích phân đó chỉ phụ thuộc vào hàm số \(f\) và các cận \(a\), \(b\) mà không phụ thuộc vào biến số \(x,t\).
b) Ý nghĩa hình học của tích phân: Nếu hàm số \(f\left(x\right)\) không âm và liên tục trên đoạn \(\left[a;b\right]\) thì tích phân \(\int_a^bf\left(x\right)dx\) là diện tích \(S\) của hình thang cong giới hạn bởi đồ thị hàm số \(f\left(x\right)\), trục \(Ox\), hai đường thẳng \(x=a,x=b\).
Vậy \(S=\int_a^bf\left(x\right)dx\).
2. Tính chất của tích phân
- Tính chất 1: \(\int_a^bk.f\left(x\right)\text{ }dx=k.\int_a^bf\left(x\right)dx\) (với k là hằng số)
- Tính chất 2: \(\int\limits^b_a\left[f\left(x\right)\pm g\left(x\right)\right]\text{ }dx=\int\limits^b_af\left(x\right)\text{dx}\pm\int\limits^b_ag\left(x\right)\text{ }dx\)
- Tính chất 3: \(\int\limits^b_af\left(x\right)\text{dx}=\int\limits^c_af\left(x\right)\text{dx}+\int\limits^b_cf\left(x\right)\text{dx}\) (\(a< c< b\))
3. Phương pháp tính tích phân
a) Phương pháp đổi biến số
Cho hàm số \(f\left(x\right)\) trên đoạn \(\left[a;b\right]\). Giả sử hàm số \(\varphi\left(t\right)\) có đạo hàm liên tục trên đoạn \(\left[\alpha;\beta\right]\)sao cho \(\varphi\left(\alpha\right)=a,\varphi\left(\beta\right)=b\) và \(a\le\varphi\left(t\right)\le b\) với mọi \(t\in\left[\alpha;\beta\right]\). Khi đó
\(\int_a^bf\left(x\right)dx=\int_{\alpha}^{\beta}f(\varphi\left(t\right))\varphi'\left(t\right)dt\)
Ví dụ: Tính \(\int_0^1\dfrac{1}{1+x^2}dx\).
Giải:
Đặt \(x=\tan t\), \(-\dfrac{\pi}{2}< t< \dfrac{\pi}{2}\). Ta có \(x'\left(t\right)=\dfrac{1}{\cos^2t}\)
Khi \(x=0\) thì \(t=0\), khi \(x=1\) thì \(t=\dfrac{\pi}{4}\)
Do đó \(\int_0^1\dfrac{1}{1+x^2}dx=\int_0^{\dfrac{\pi}{4}}\dfrac{1}{1+\tan^2t}.\dfrac{dt}{\cos^2t}=\int_0^{\dfrac{\pi}{4}}dt=\dfrac{\pi}{4}\).
b) Phương pháp tính tích phân từng phần
Nếu \(u=u\left(x\right)\) và \(v=v\left(x\right)\) là hai hàm số liên tục trên đoạn \(\left[a;b\right]\) thì
\(\int_a^bu\left(x\right)v'\left(x\right)dx=\left(u\left(x\right)v\left(x\right)\right)|^b_a-\int_a^bu'\left(x\right)v\left(x\right)dx\)
hay \(\int_a^budv=uv|^b_a-\int_a^bvdu\).
Ví dụ: Tính \(\int_0^{\dfrac{\pi}{2}}x\sin xdx\).
Giải:
Đặt \(u=x\) và \(dv=\sin xdx\) , ta có \(du=dx\) và \(v=-\cos x\)
Do đó: \(\int_0^{\dfrac{\pi}{2}}x\sin xdx=\left(-x\cos x\right)|^{\dfrac{\pi}{2}}_0+\int_0^{\dfrac{\pi}{2}}\cos xdx\)
\(=\left(-x\cos x\right)|^{\dfrac{\pi}{2}}_0+\left(\sin x\right)|^{\dfrac{\pi}{2}}_0=0+1=1\).
@75775@
III. ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
1. Tính diện tích hình phẳng
a) Hình phẳng giới hạn bởi một đường cong và trục hoành
Một cách tổng quát, diện tích \(S\) của hình phẳng giới hạn bởi đồ thị của hàm số \(f\left(x\right)\) liên tục, trục hoành và hai đường thẳng \(x=a,x=b\) được tính theo công thức:
\(S=\int_a^b\left|f\left(x\right)\right|dx\)
Ví dụ: Tính diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \(y=x^3\), trục hoành và hai đường thẳng \(x=-1,x=2\).
Giải:
Ta có \(x^3\le0\) trên đoạn \(\left[-1;0\right]\) và \(x^3\ge0\) trên đoạn \(\left[0;2\right]\). Áp dụng công thức trên ta có:
\(S=\int_{-1}^2\left|x^3\right|dx=\int_{-1}^0\left(-x^3\right)dx+\int_0^2x^3dx\)
\(=-\dfrac{x^4}{4}|^0_{-1}+\dfrac{x^4}{4}|^2_0=\dfrac{17}{4}\)
b) Hình phẳng giới hạn bởi hai đường cong
Cho hai hàm số \(y=f_1\left(x\right)\) và \(y=f_2\left(x\right)\) liên tục trên đoạn \(\left[a;b\right]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hai hàm số đó và hai đường thẳng \(x=a,x=b\).
Khi đó diện tích \(S\) của hình \(D\) được tính bởi công thức:
\(S=\int_a^b\left|f_1\left(x\right)-f_2\left(x\right)\right|dx\)
Chú ý: Muốn áp dụng được công thức này ta cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Ta giải phương trình \(f_1\left(x\right)-f_2\left(x\right)=0\) trên đoạn \(\left[a;b\right]\). Giả sử phương trình có hai nghiệm \(c,d\left(c< d\right)\). Khi đó \(f_1\left(x\right)-f_2\left(x\right)\) không đổi dấu trên từng đoạn \(\left[a;c\right],\left[c;d\right],\left[d;b\right]\). Trên mỗi đoạn đó, chẳng hạn đoạn \(\left[a;c\right]\), ta có
\(\int_a^c\left|f_1\left(x\right)-f_2\left(x\right)\right|dx=\left|\int_a^c\left[f_1\left(x\right)-f_2\left(x\right)\right]dx\right|\)
Ví dụ: Tính diện tích hình phẳng giới hạn bởi hai đường thẳng \(x=0,x=\pi\) và đồ thị của hai hàm số \(y=\cos x,y=\sin x\).
Giải:
Đặt \(f_1\left(x\right)=\cos x,f_2\left(x\right)=\sin x\)
Ta có \(f_1\left(x\right)-f_2\left(x\right)=0\Leftrightarrow\cos x-\sin x=0\Leftrightarrow x=\dfrac{\pi}{4}\in\left[0;\pi\right]\)
Vậy diện tích của hình phẳng đã cho là:
\(S=\int_0^{\pi}\left|\cos x-\sin x\right|dx=\int_0^{\dfrac{\pi}{4}}\left|\cos x-\sin x\right|dx+\int_{\dfrac{\pi}{4}}^{\pi}\left|\cos x-\sin x\right|dx\)
\(=\left|\int_0^{\dfrac{\pi}{4}}(\cos x-\sin x)dx\right|+\left|\int_{\dfrac{\pi}{4}}^{\pi}(\cos x-\sin x)dx\right|\)
\(=\left|\left(\sin x+\cos x\right)|^{\dfrac{\pi}{4}}_0\right|+\left|\left(\sin x+\cos x\right)|^{\pi}_{\dfrac{\pi}{4}}\right|=2\sqrt{2}\)
2. Tính thể tích
a) Thể tích của vật thể
Cắt một vật thể \(\lambda\) bởi hai mặt phẳng \(\left(P\right)\) và \(\left(Q\right)\) vuông góc với trục hoành lần lượt tại \(x=a,x=b\) \(\left(a< b\right)\). Một mặt phẳng tuỳ ý vuông góc với trục hoành tại điểm \(x\) (\(a\le x\le b\)) cắt \(\lambda\) bởi một thiết diện có diện tích \(S\left(x\right)\). Giả sử \(S\left(x\right)\) liên tục trên đoạn \(\left[a;b\right]\).
Người ta chứng minh được rằng thể tích \(V\) của phần vật thể \(\lambda\) giới hạn bởi hai mặt phẳng \(\left(P\right)\) và \(\left(Q\right)\) được tính bởi công thức:
\(V=\int_a^bS\left(x\right)dx\)
b) Thể tích khối chóp và khối chóp cụt
- Cho khối chóp có chiều cao bằng \(h\) và diện tích đáy bằng \(B\).
Chọn trục \(Ox\) vuông góc với mặt phẳng đáy tại điểm \(I\) sao cho gốc \(O\) trùng với đỉnh của khối chóp và có hướng xác định bởi vectơ \(\overrightarrow{OI}\). Khi đó \(OI=h\). Một mặt phẳng \(\left(\alpha\right)\) vuông góc với \(Ox\) tại \(x\left(0\le x\le h\right)\) cắt khối chóp theo thiết diện có diện tích là \(S\left(x\right)\).
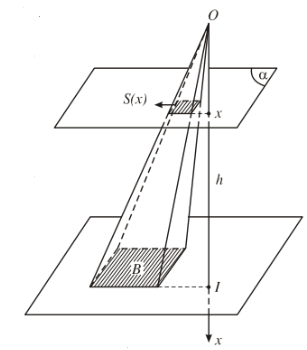
Khi đó thể tích \(V\) của khối chóp được tính bởi công thức:
\(V=\int_0^hS\left(x\right)dx=\int_0^hB\dfrac{x^2}{h^2}dx=\dfrac{B}{h^2}\left(\dfrac{x^3}{3}\right)|^h_0=\dfrac{Bh}{3}\)
- Cho hình chóp cụt tạo bởi khối chóp đỉnh \(S\) có diện tích hai đáy lần lượt là \(B,B'\) và chiều cao \(h\).
Chọn trục \(Ox\) trùng với đường cao của hình chóp và gốc \(O\) trùng với đỉnh \(S\). Hai mặt phẳng đáy của hình chóp cụt cắt trục \(Ox\) tại \(I\) và \(I'\). Đặt \(OI=b,OI'=a\left(a< b\right)\). Gọi \(V\) là thể tích của hình chóp cụt. Ta có:
\(V=\int_a^bB\dfrac{x^2}{b^2}dx=\dfrac{B}{3b^2}\left(b^3-a^3\right)=B.\dfrac{b-a}{3}.\dfrac{a^2+ab+b^2}{b^2}\)
Vì \(B'=B\dfrac{a^2}{b^2}\) và \(h=b-a\) nên
\(V=\dfrac{h}{3}\left(B+\sqrt{BB'}+B'\right)\)
3. Thể tích khối tròn xoay
Giả sử một hình thang cong giới hạn bởi đồ thị hàm số \(y=f\left(x\right)\), trục \(Ox\) và hai đường thẳng \(x=a,x=b\) quay quanh trục \(Ox\) tạo thành một khối tròn xoay. Khi đó thể tích \(V\) của khối tròn xoay đó được tính bởi công thức:
\(V=\pi\int_a^bf^2\left(x\right)dx\).
Ví dụ: Cho hình phẳng giới hạn bởi đồ thị \(y=\sin x\), trục hoành và hai đường thẳng \(x=0,x=\pi\). Tính thể tích khối tròn xoay thu được khi quay hình phẳng trên quanh trục \(Ox\).
Giải:
Áp dụng công thức trên ta có thể tích khối tròn xoay cần tính là:
\(V=\pi\int_0^{\pi}\sin^2xdx=\dfrac{\pi}{2}\int_0^{\pi}\left(1-\cos2x\right)dx=\dfrac{\pi}{2}\left(x-\dfrac{1}{2}\sin2x\right)|^{\pi}_0=\dfrac{\pi^2}{2}\).
@75857@