Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông

1. Các hệ thức

Cho tam giác \(ABC\) vuông tại \(A\), cạnh huyền \(BC=a\), các cạnh góc vuông \(AB=c;AC=b\). 

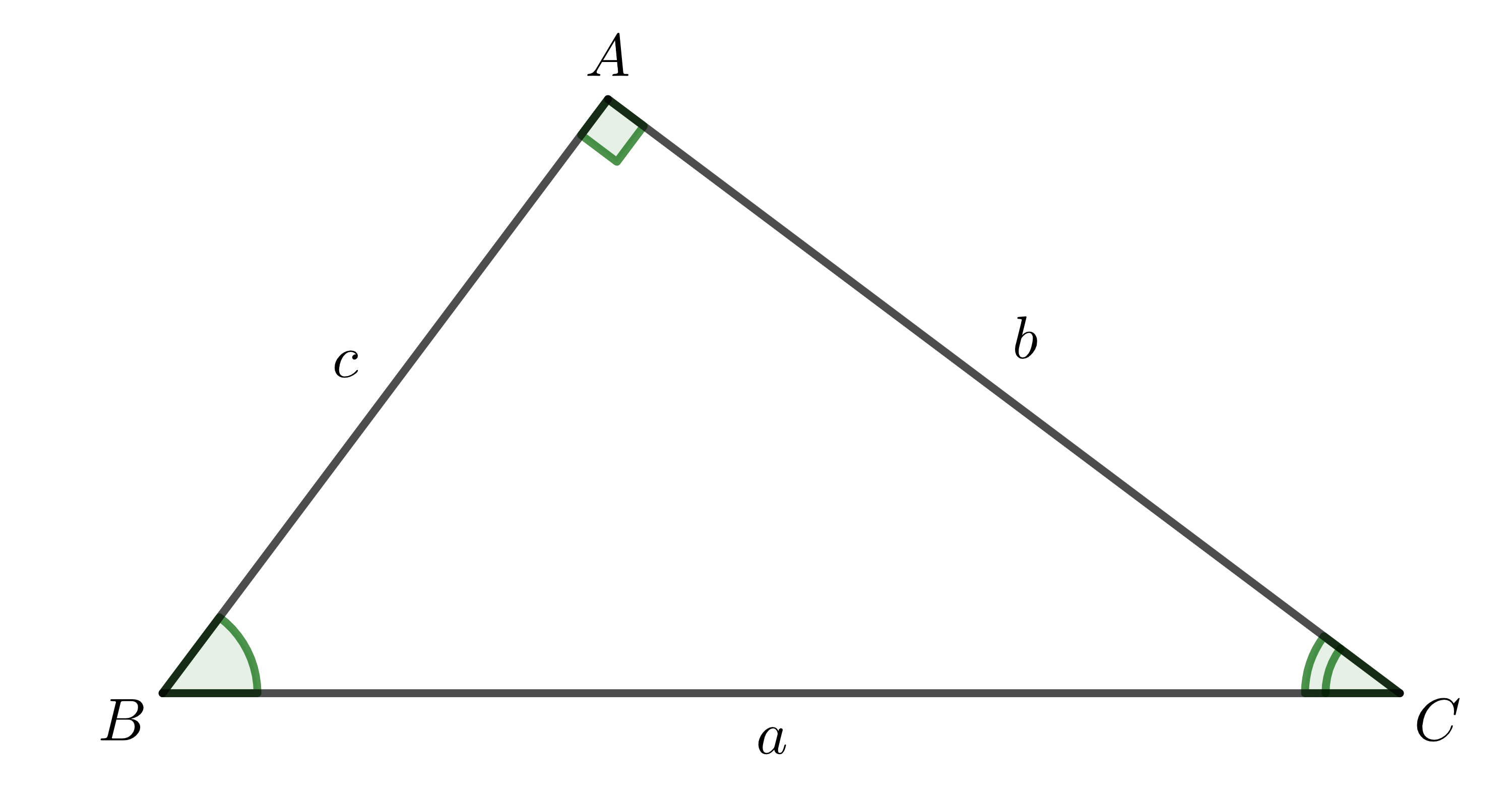
Sử dụng tỉ số lượng giác ở bài trước, ta có:

\(\sin B=\dfrac{b}{a}\Rightarrow b=a.\sin B\); \(\sin C=\dfrac{c}{a}\Rightarrow c=a.\sin C\)

\(\cos B=\dfrac{c}{a}\Rightarrow c=a.\cos B\); \(\cos C=\dfrac{b}{a}\Rightarrow b=a.\cos C\)

\(\tan B=\dfrac{b}{c}\Rightarrow b=c.\tan B\); \(\tan C=\dfrac{c}{b}\Rightarrow c=b.\tan C\)

\(\cot B=\dfrac{c}{b}\Rightarrow c=b.\cot B\); \(\cot C=\dfrac{b}{c}\Rightarrow b=c.\cot C\)

Các kết quả trên không phụ thuộc vào hình dạng, kích thước tam giác \(ABC\).

Như vậy, ta có định lí: 

Trong tam giác vuông, mỗi cạnh góc vuông bằng:

• Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
• Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

Cụ thể, trong tam giác \(ABC\) như trên:

\(b=a.\sin B=a.\cos C=c.\tan B=c.\cot C\)

\(c=a.\sin C=a.\cos B=b.\tan C=b.\cot B\)

Kết quả này được ứng dụng trong nhiều bài toán thực tế.

Ví dụ 1: Một cái thang dài \(3m\). Biết rằng, để thang không đổ thì nó cần được dựng sao cho tạo với mặt đất một góc an toàn \(65^0\). Hỏi chân thang cách tường một khoảng bao nhiêu?

Lời giải:

Ta biểu diễn bài toán bằng hình vẽ sau: 

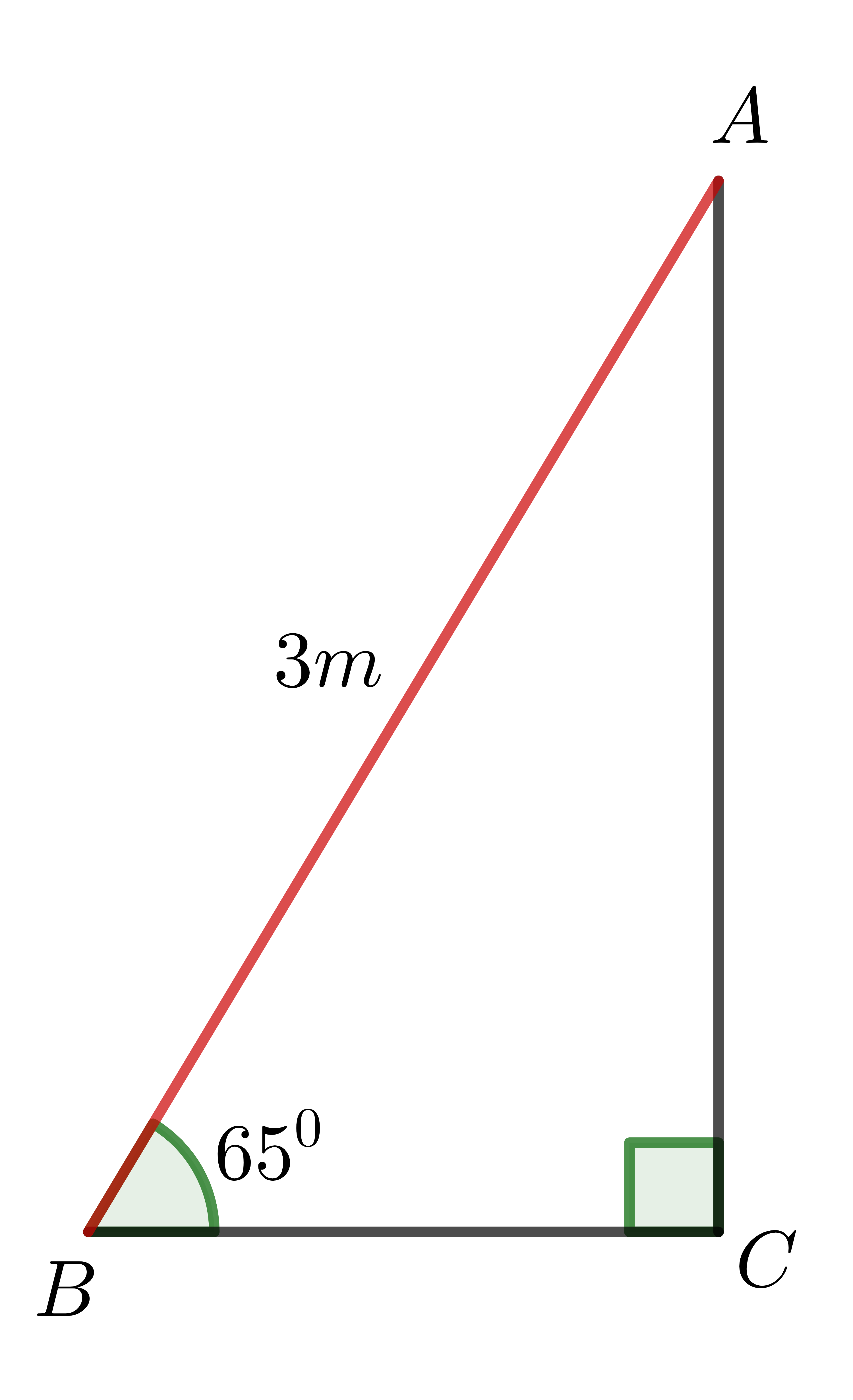
trong đó, \(AB\) biểu diễn vị trí của thang, \(BC\) là khoảng cách từ chân thang đến tường.

Ta có: \(BC=AB.\cos B\Rightarrow BC=3.\cos65^0\approx1,268\left(m\right)\).

Vậy, chân thang cách tường một khoảng xấp xỉ \(1,268m\).

Ví dụ 2: Một máy bay bay lên từ mặt đất với vận tốc \(500\) km/h. Đường bay hợp với phương ngang một góc \(30^0\). Hỏi mất bao lâu thì máy bay đạt đến độ cao \(100\)km so với mặt đất?

Lời giải:

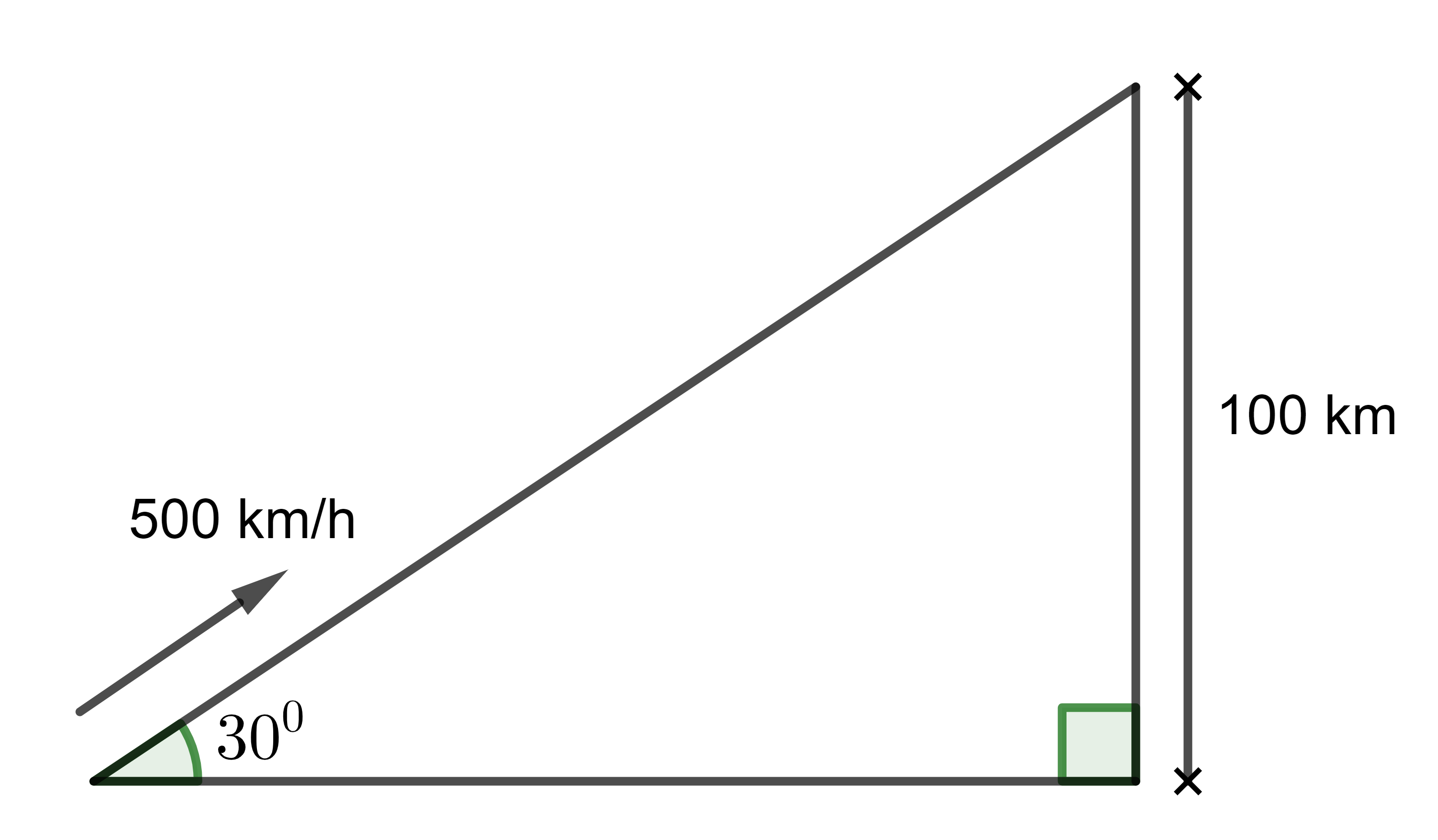
Đường bay của máy bay chính là cạnh huyền trong tam giác vuông trên.

Gọi độ dài đoạn đường bay cho đến khi máy bay đạt được độ cao 100 km so với mặt đất là \(s\). Ta có:

\(100=s.\sin30^0\Rightarrow s=\dfrac{100}{\sin30^0}=200\)(km).

Vận tốc của máy bay là \(v=500\) (km/h)

\(\Rightarrow\) Thời gian bay từ khi cất cánh đến khi đạt được độ cao 100 km so với mặt đất là:

\(t=\dfrac{s}{v}=\dfrac{200}{500}=0,4\left(h\right)=24\) (phút).

2. Áp dụng giải tam giác vuông

Bài toán giải tam giác vuông là bài toán đi tìm tất cả các cạnh và góc chưa biết trong một tam giác vuông, khi ta đã biết hai cạnh hoặc một cạnh và một góc nhọn của nó.

Ví dụ 1: Tam giác \(MNP\) vuông tại \(M\), có \(MN=5;MP=12\). Hãy giải tam giác vuông \(MNP\).

Lời giải:

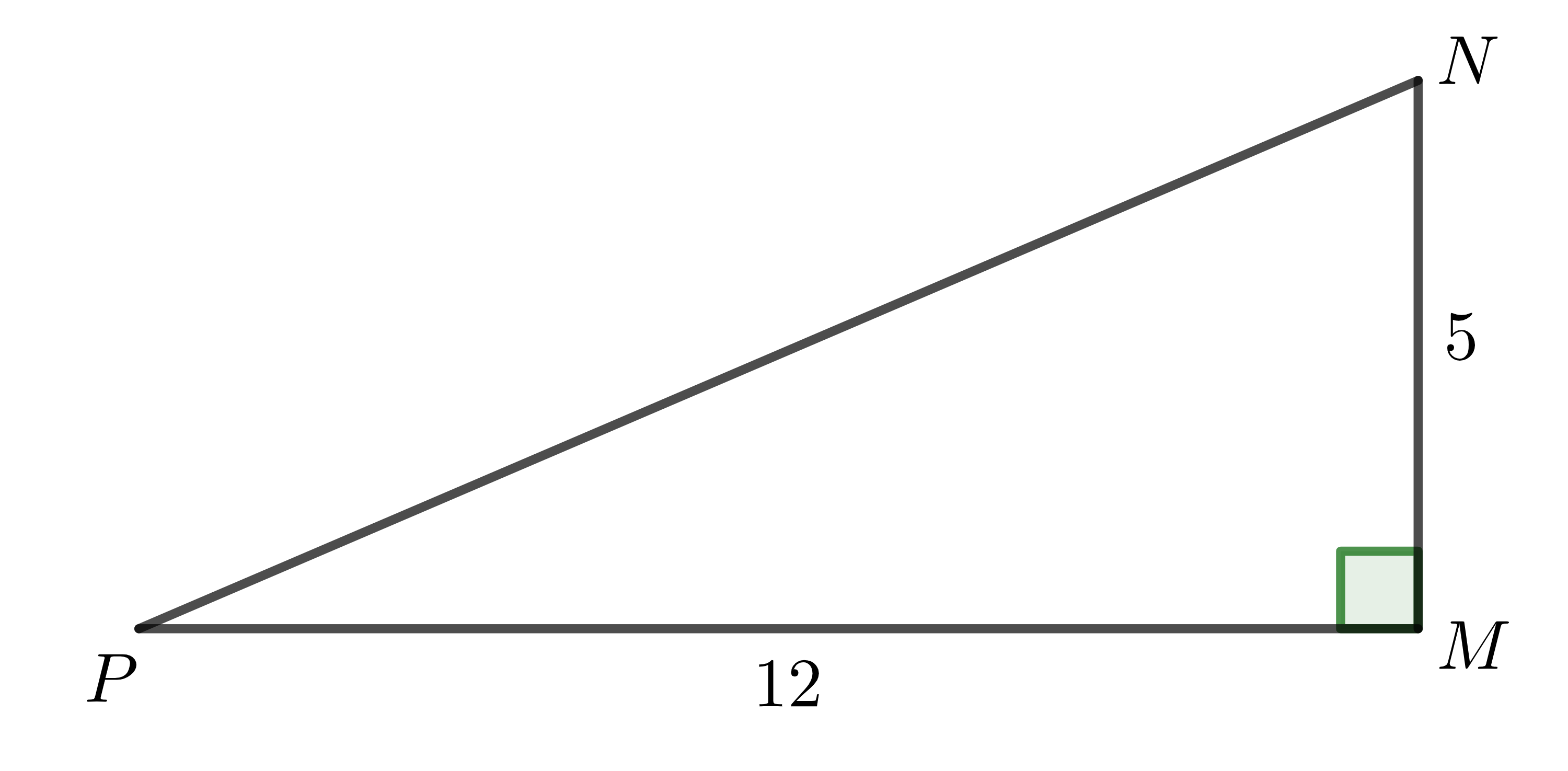
Áp dụng định lí Pytago, ta có: \(NP^2=MN^2+MP^2\)

\(\Rightarrow NP=\sqrt{MP^2+MN^2}=\sqrt{5^2+12^2}=13\).

Ta có: \(\sin P=\dfrac{MN}{NP}=\dfrac{5}{13}\Rightarrow\widehat{P}\approx23^0\)

\(\Rightarrow\widehat{N}\approx90^0-23^0=67^0\).

Ví dụ 2: Giải tam giác \(ABC\) biết tam giác vuông tại \(A\), \(AB=5\), \(B=40^0\).

Lời giải:

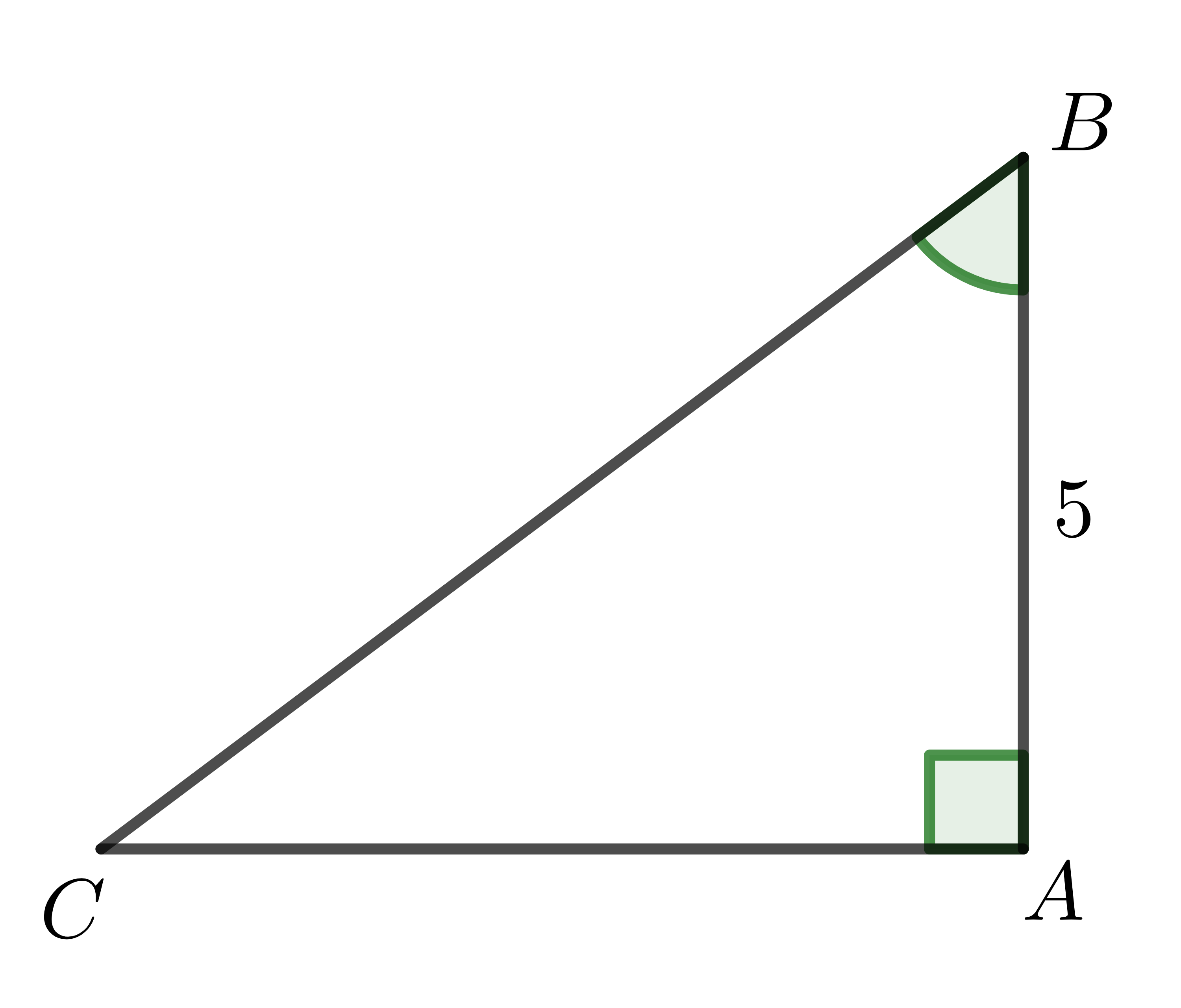
Ta có: \(\widehat{C}=90^0-\widehat{B}=90^0-40^0=50^0\).

Mặt khác, ta lại có:

\(\left\{{}\begin{matrix}AC=AB.\tan B=5.\tan40^0\approx4,195\\AB=BC.\sin C\Rightarrow BC=\dfrac{AB}{\sin C}=\dfrac{5}{\sin50^0}\approx6,527\end{matrix}\right.\).

Chú ý: Trong quá trình giải tam giác vuông, ta cần hạn chế tối đa việc sử dụng các kết quả là tròn trung gian để sai số là nhỏ nhất.