Bài 4: Góc tạo bởi tiếp tuyến và dây cung

1. Khái niệm góc tạo bởi tiếp tuyến và dây cung

+) Cho \(xy\) là tiếp tuyến của đường tròn \(\left(O\right)\), tiếp điểm tại \(A\). Khi đó, \(Ax\) và \(Ay\) gọi là các tia tiếp tuyến.

Khái niệm: Góc tạo bởi tiếp tuyến và dây cung là góc

• Có đỉnh nằm trên đường tròn;
• Một cạnh là tia tiếp tuyến;
• Một cạnh chứa dây cung của đường tròn.

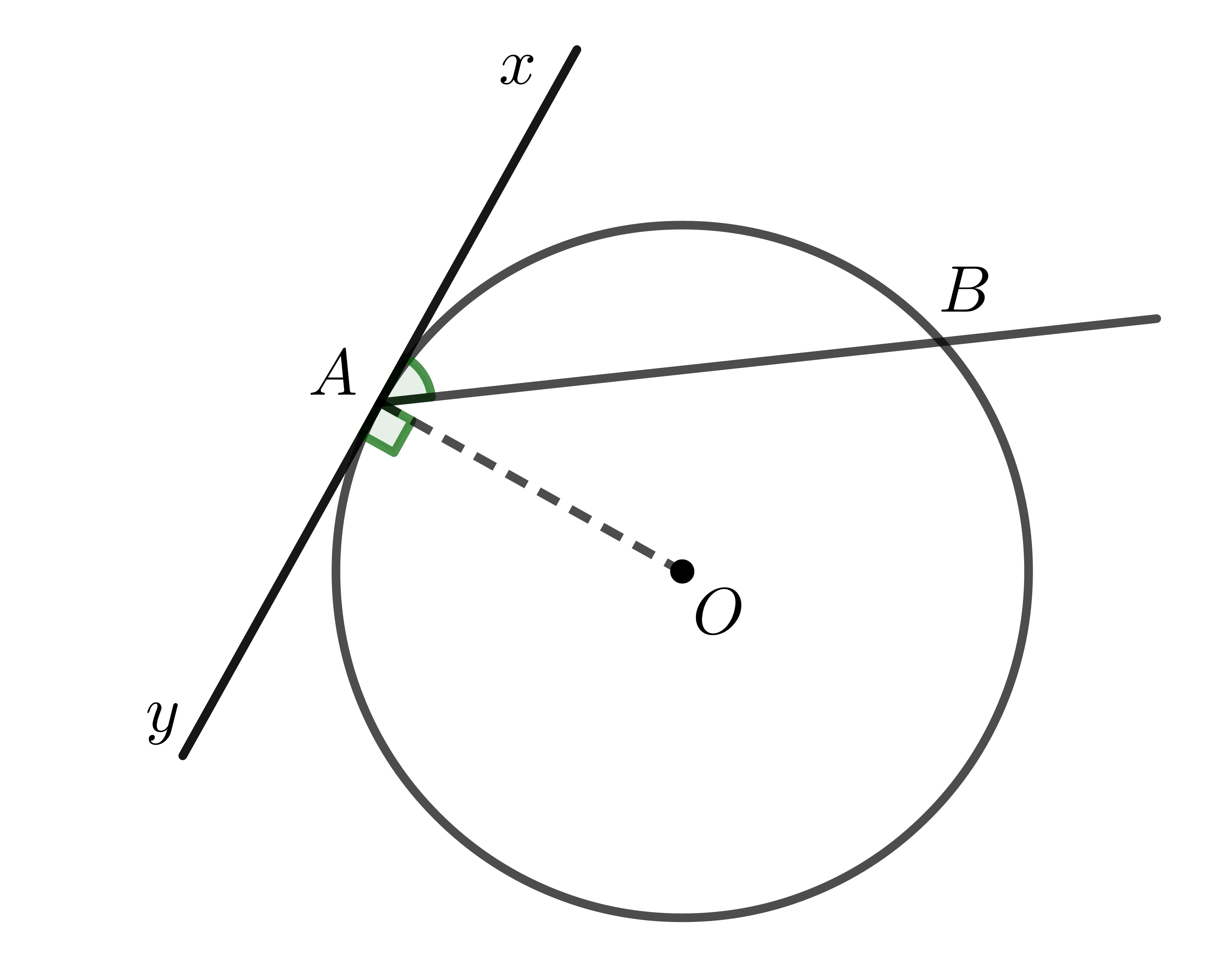
+) Góc \(BAx\) (hoặc góc \(BAy\)) có đỉnh \(A\) nằm trên đường tròn, một cạnh là tia tiếp tuyến \(Ax\) (hoặc \(Ay\)), cạnh kia chứa dây cung \(AB\) của đường tròn \(\left(O\right)\). Khi đó, góc \(BAx\) (hoặc góc \(BAy\)) được gọi là góc tạo bởi tiếp tuyến và dây cung.

+) Cung nằm bên trong góc gọi là cung bị chắn.

Ví dụ: Trong hình trên, góc \(BAx\) có cung bị chắn là cung \(AB\) nhỏ, góc \(BAy\) có cung bị chắn là cung \(AB\) lớn.

Ví dụ: Các góc sau đây không phải là góc tạo bởi tiếp tuyến và dây cung:

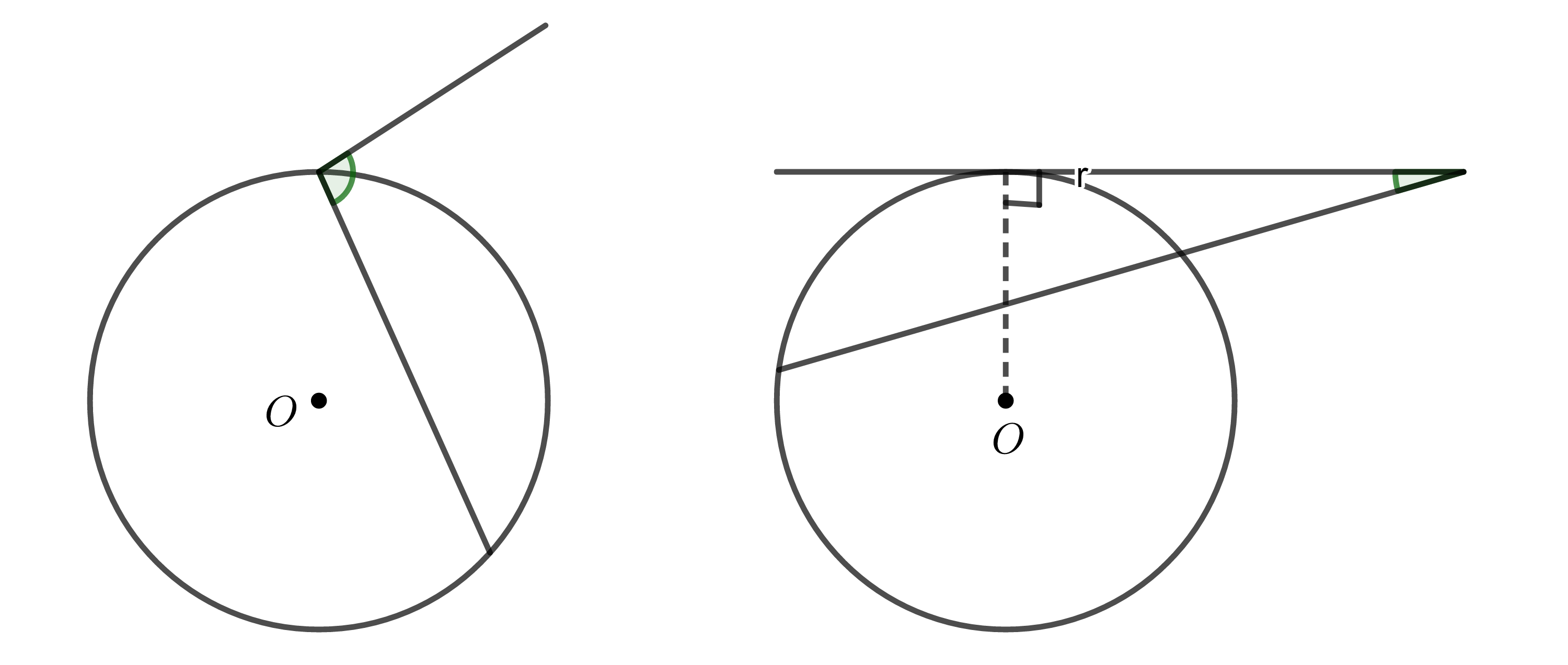
2. Định lí

Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.

Ta chứng minh định lí trên bằng cách xét 3 trường hợp:

a) Trường hợp 1: Tâm đường tròn nằm trên cạnh chứa dây cung

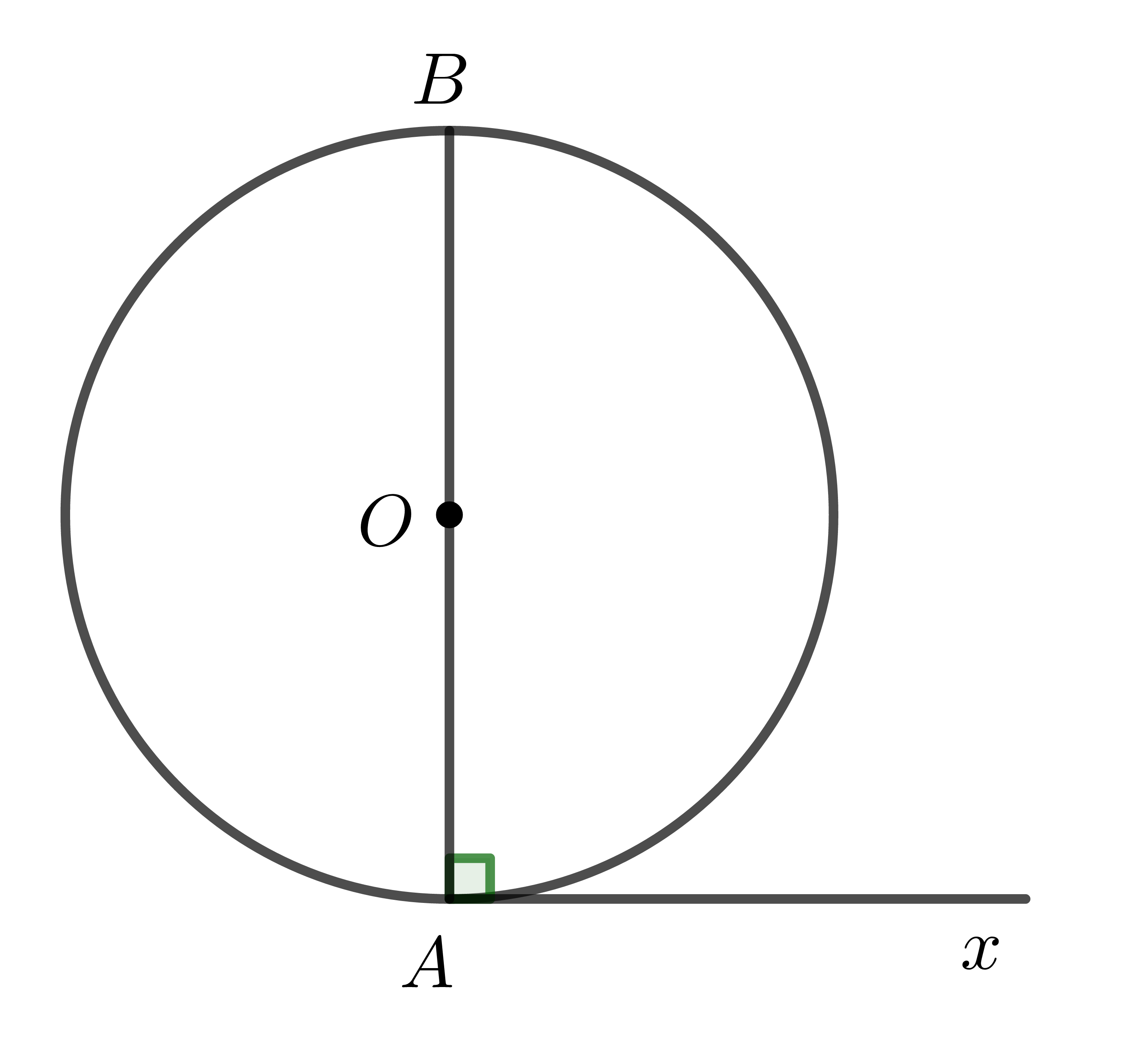
Ta có: \(\widehat{BAx}=90^0\), \(sđ\stackrel\frown{AB}=180^0\) 

\(\Rightarrow\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (định lí được chứng minh).

b) Trường hợp 2: Tâm đường tròn nằm bên ngoài góc

Kẻ \(OH\) vuông góc \(AB\).

Ta có: \(\widehat{BAx}=\widehat{O_1}\) (cùng phụ với \(\widehat{OAB}\)).

Lại có: tam giác \(OAB\) cân tại \(O\Rightarrow OH\) là phân giác \(\widehat{AOB}\)

\(\Rightarrow\widehat{O_1}=\dfrac{1}{2}.\widehat{AOB}\Rightarrow\widehat{BAx}=\dfrac{1}{2}.\widehat{AOB}\) 

Mà \(\widehat{AOB}=sđ\stackrel\frown{AmB}\) (tính chất góc ở tâm) \(\Rightarrow\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AmB}\).

c) Trường hợp 3: Tâm đường tròn nằm bên trong góc

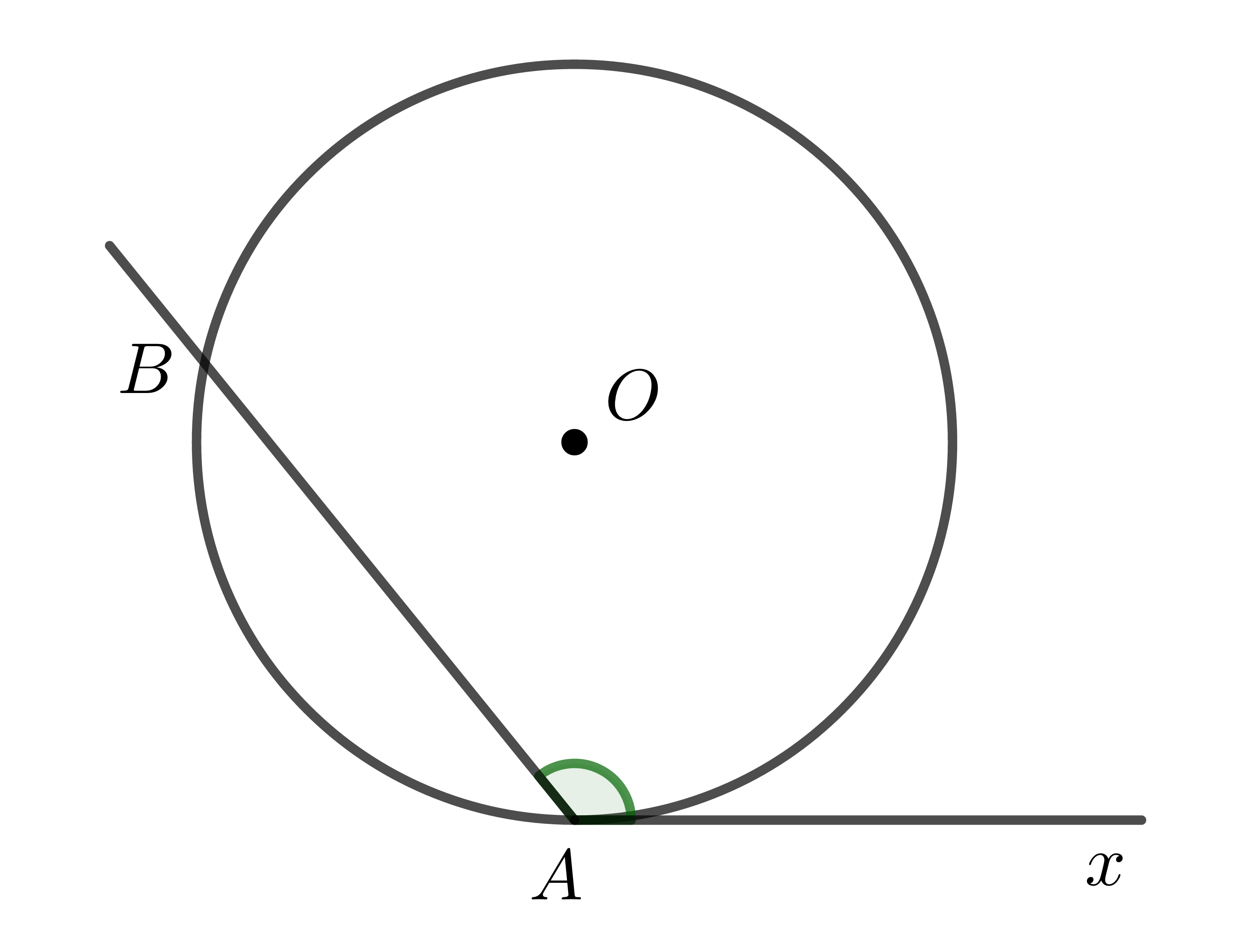
Kẻ tia tiếp tuyến \(Ay\) là tia đối của tia \(Ax\).

Theo trường hợp 2: \(\widehat{BAy}\) bằng nửa số đo cung nhỏ \(AB\).

Mặt khác, \(\widehat{BAx}=180^0-\widehat{BAy}\).

Từ biểu thức trên và kết quả từ trường hợp 2, ta dễ dàng thu được điều cần chứng minh.

3. Hệ quả

Theo định lí: góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn

Theo tính chất góc nội tiếp, góc nội tiếp bằng nửa số đo cung bị chắn 

\(\Rightarrow\) Ta thu được hệ quả:

Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn một cung.

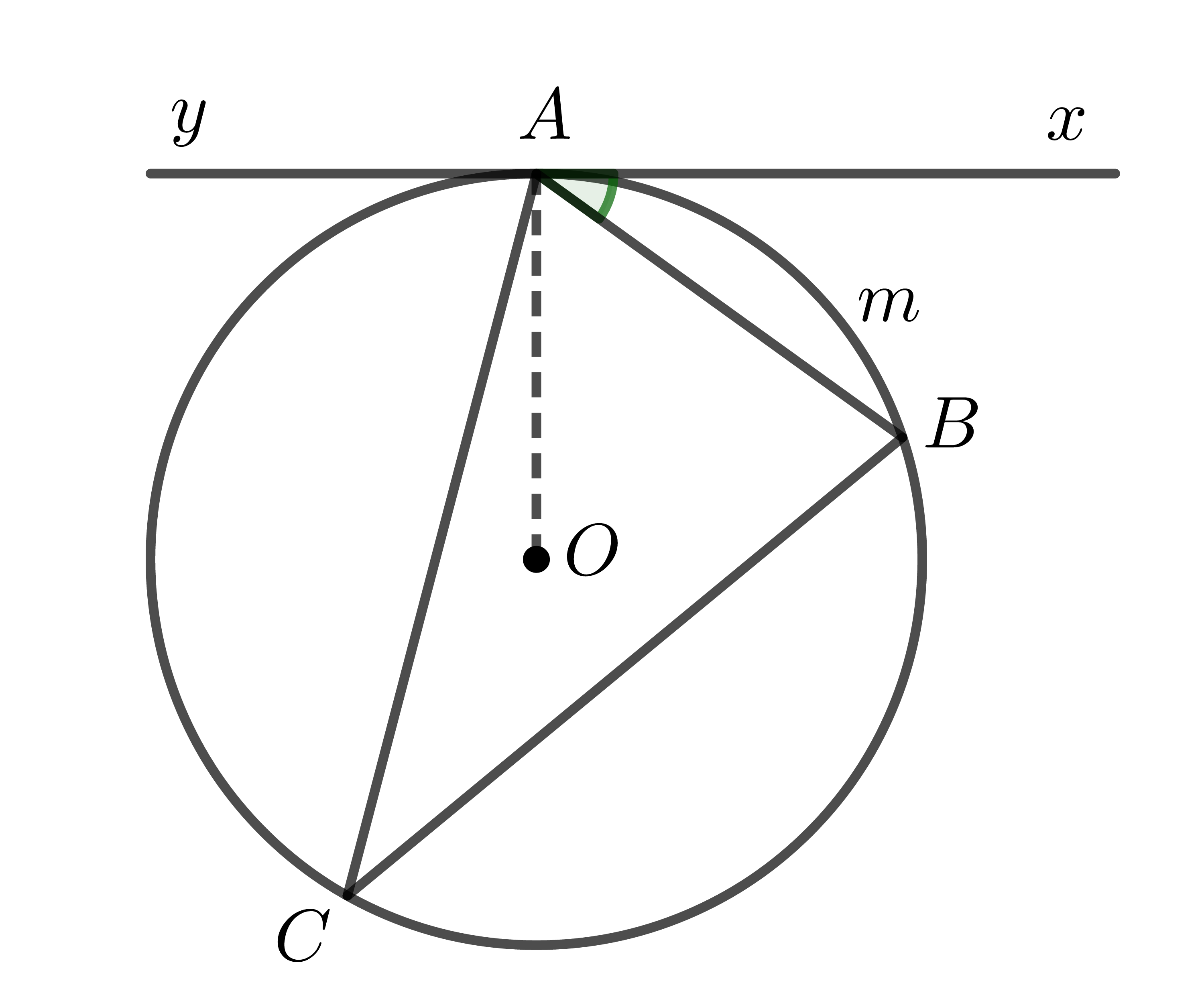
Trong hình trên: \(\widehat{BAx}=\widehat{ACB}=\dfrac{1}{2}sđ\stackrel\frown{AmB}\).