Bài 3: Diện tích tam giác

1. Định lí

Để tính diện tích một tam giác bất kì, ta sử dụng định lí sau:

Định lí: Diện tích tam giác bằng nửa tích một cạnh với chiều cao ứng với cạnh đó.

\(S=\dfrac{1}{2}a.h\)

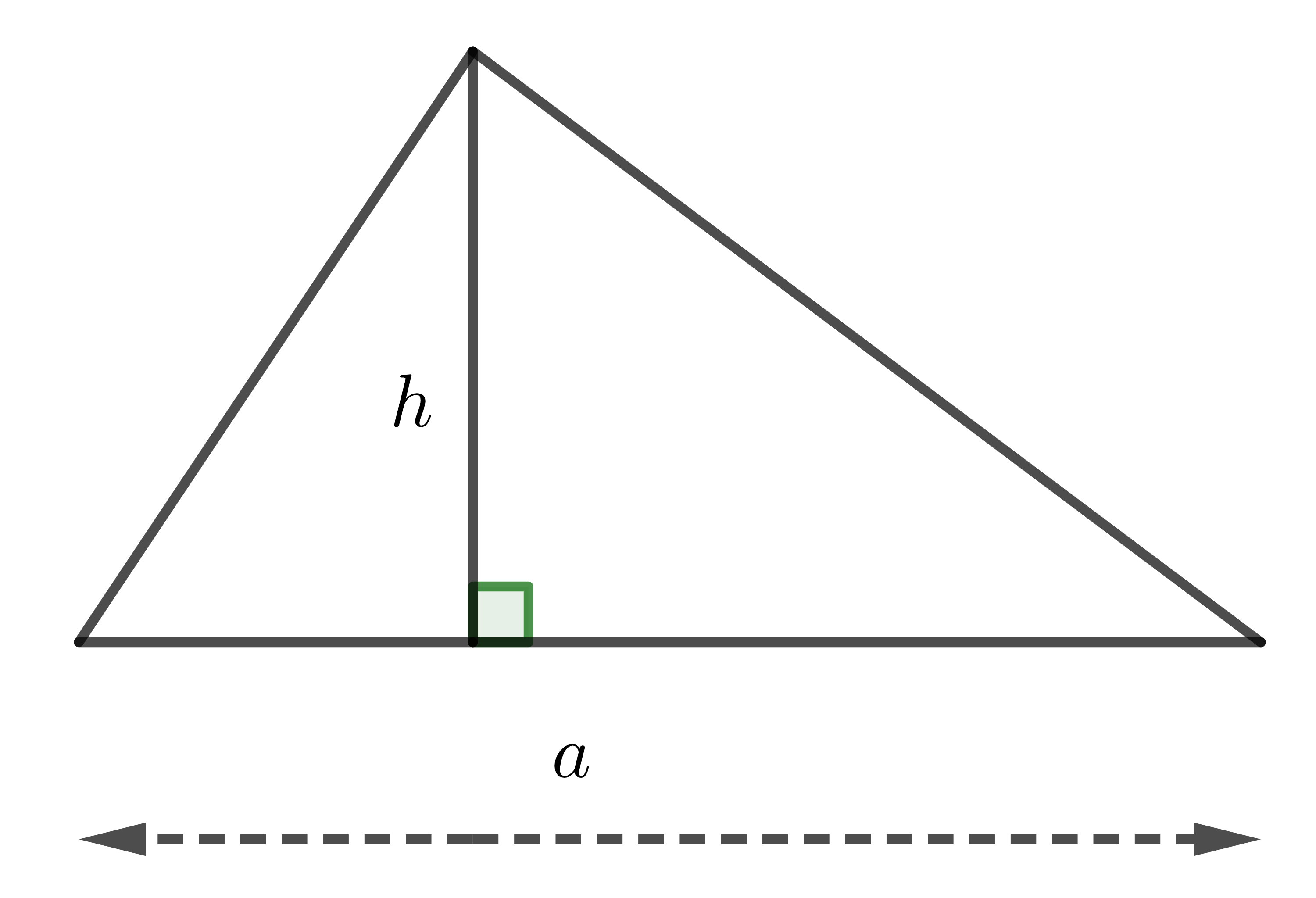
Chứng minh:

Xét tam giác \(ABC\), \(AH\perp BC\). Ta cần chứng minh \(S_{ABC}=\dfrac{1}{2}AH.BC\).

Để chứng minh, ta chia thành 3 trường hợp:

a) Trường hợp 1: Điểm \(H\) trùng với \(B\) hoặc \(C\).

Không mất tính tổng quát, giả sử \(H\equiv B\).

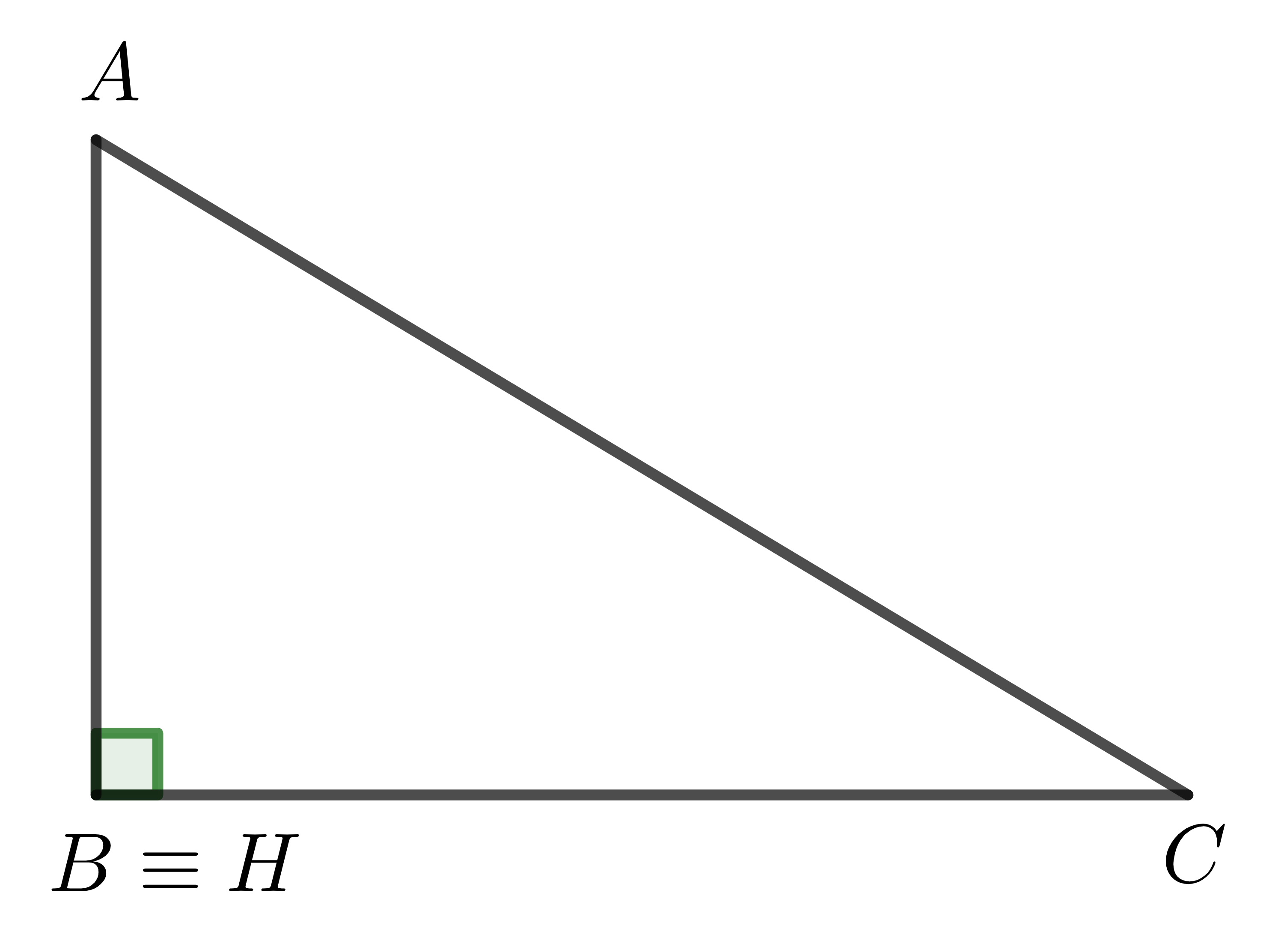
Trong trường hợp này, tam giác \(ABC\) vuông tại \(B\). Theo bài trước, ta có: 

\(S_{ABC}=\dfrac{1}{2}AB.BC=\dfrac{1}{2}AH.BC\) (Điều phải chứng minh).

b) Trường hợp 2: Điểm \(H\) nằm giữa \(B\) và \(C\).

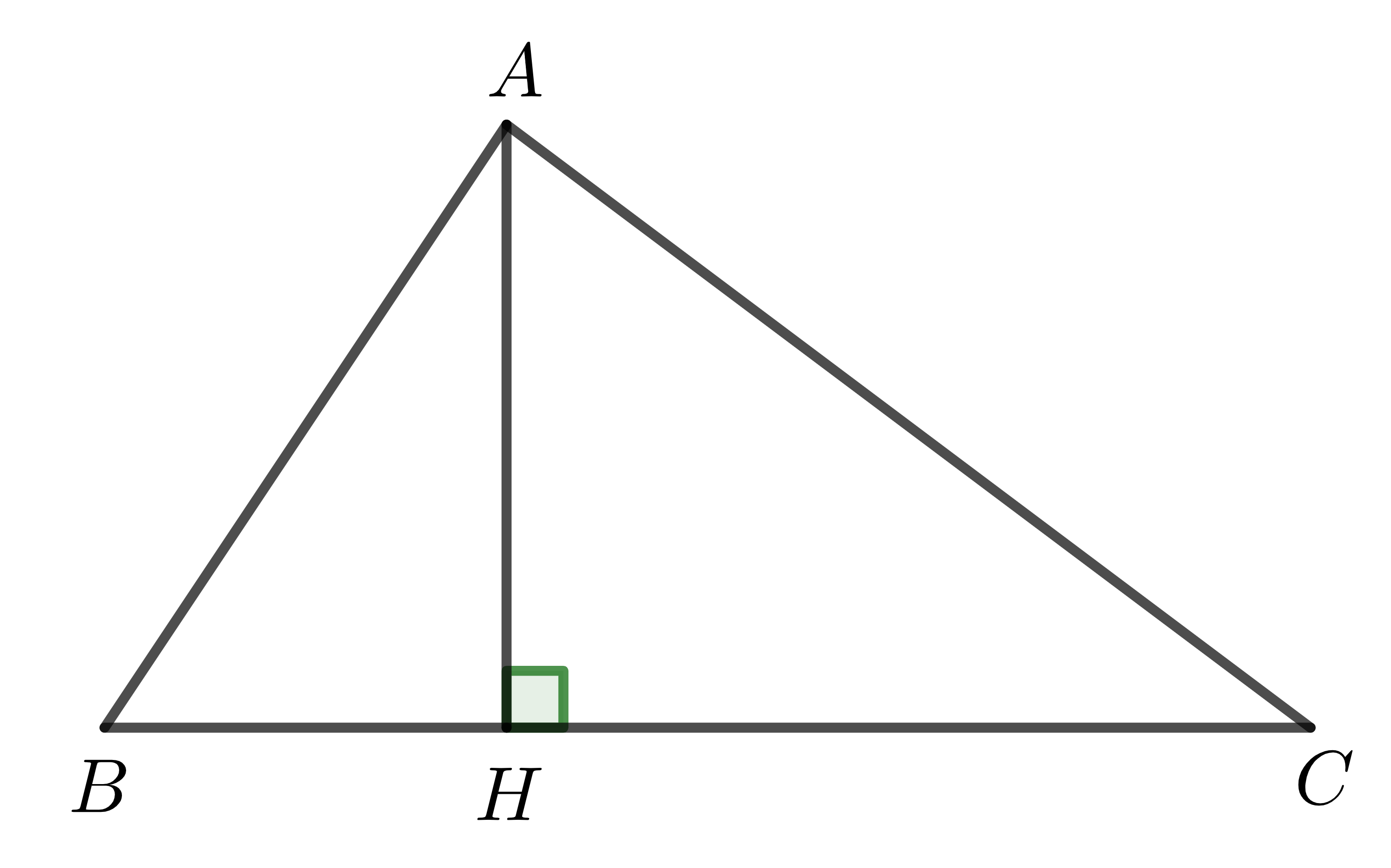
Trong trường hợp này, tam giác \(ABC\) được chia thành hai tam giác \(ABH\) và \(ACH\).

Do đó, theo bài trước, ta có:

\(S_{ABC}=S_{ABH}+S_{ACH}\\ =\dfrac{1}{2}AH.BH+\dfrac{1}{2}AH.CH=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}AH.BC\)

Như vậy, ta được điều cần chứng minh.

c) Trường hợp 3: Điểm \(H\) nằm ngoài đoạn thẳng \(BC\).

Không mất tính tổng quát, giả sử \(C\) nằm giữa \(H\) và \(B\).

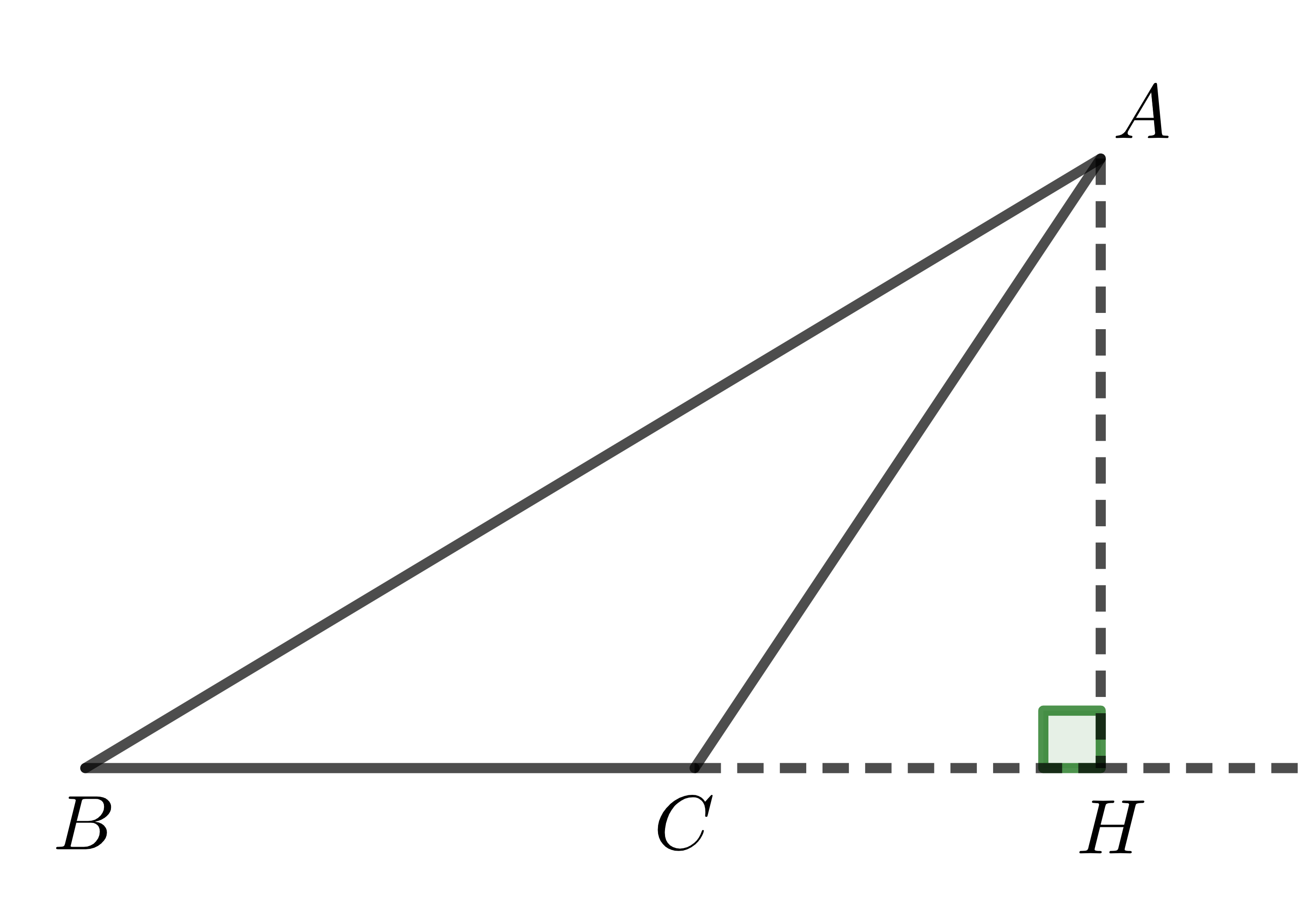
Trong trường hợp này, tam giác \(ABH\) được chia thành hai tam giác \(ABC\) và \(ACH\).

Do đó, ta có: \(S_{ABH}=S_{ABC}+S_{ACH}\)

\(\Rightarrow S_{ABC}=S_{ABH}-S_{ACH}\\ =\dfrac{1}{2}AH.BH-\dfrac{1}{2}AH.CH=\dfrac{1}{2}AH\left(BH-CH\right)=\dfrac{1}{2}AH.BC\)

Ta được điều phải chứng minh.

2. Áp dụng

Ví dụ 1: Cho tam giác \(ABC\), đường cao \(AH\). Biết \(BC=4cm\), \(AH=3cm\). Khi đó, diện tích tam giác \(ABC\) là: \(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.3.4=6\left(cm^2\right)\).

Ví dụ 2: Cho tam giác \(ABC\), \(M\) là trung điểm \(BC\). Biết diện tích tam giác \(ABC\) là \(100cm^2\). Tính diện tích tam giác \(ABM\)?

Lời giải:

Kẻ \(AH\perp BC\). Dễ thấy, \(AH\) cũng là đường cao của tam giác \(ABM\).

Ta có: \(S_{ABM}=\dfrac{1}{2}AH.BM;S_{ABC}=\dfrac{1}{2}AH.BC\)

Mà \(BM=\dfrac{1}{2}BC\) (giả thiết) \(\Rightarrow\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{BM}{BC}=\dfrac{1}{2}\Rightarrow S_{ABM}=\dfrac{1}{2}.S_{ABC}=\dfrac{1}{2}.100=50\left(cm^2\right)\).

Vậy diện tích tam giác \(ABM\) là \(50cm^2\).

Nhận xét: Từ ví dụ trên, ta có nhận xét:

• Nếu hai tam giác có cùng đường cao thì tỉ số diện tích của chúng bằng tỉ số hai cạnh đáy tương ứng với đường cao đó.
• Ngược lại, nếu hai tam giác có cùng cạnh đáy thì tỉ số diện tích của chúng bằng tỉ số hai đường cao ứng với cạnh đáy đó.