Bài 2: Phương trình mặt phẳng

I. VECTƠ PHÁP TUYẾN CỦA MẶT PHẲNG

Định nghĩa:

Cho mặt phẳng \(\left(\alpha\right)\). Nếu vectơ \(\overrightarrow{n}\) khác \(\overrightarrow{0}\) và có giá vuông góc với mặt phẳng \(\left(\alpha\right)\) thì \(\overrightarrow{n}\) được gọi là vectơ pháp tuyến của mặt phẳng \(\left(\alpha\right)\).

Chú ý: Nếu \(\overrightarrow{n}\) là vectơ pháp tuyến của mặt phẳng \(\left(\alpha\right)\) thì \(k\overrightarrow{n}\) với \(k\ne0\) cũng là vectơ pháp tuyến của mặt phẳng đó.

Trong không gian \(Oxyz\) cho mặt phẳng \(\left(\alpha\right)\) và hai vectơ không cùng phương \(\overrightarrow{a}=\left(a_1;a_2;a_3\right)\) và \(\overrightarrow{b}=\left(b_1;b_2;b_3\right)\) có giá song song hoặc nằm trong mặt phẳng \(\left(\alpha\right)\). Khi đó mặt phẳng \(\left(\alpha\right)\) nhận vectơ 

                \(\overrightarrow{n}=\left(a_2b_3-a_3b_2;a_3b_1-a_1b_3;a_1b_2-a_2b_1\right)\)

làm vectơ pháp tuyến.

Vectơ \(\overrightarrow{n}\) xác định như trên được gọi là tích có hướng (hay tích vectơ) của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\), kí hiệu là \(\overrightarrow{n}=\overrightarrow{a}\Lambda\overrightarrow{b}\) hoặc \(\overrightarrow{n}=\left[\overrightarrow{a},\overrightarrow{b}\right]\).

Ví dụ 1: Trong không gian \(Oxyz\) cho ba điểm \(A\left(2;-1;3\right),B\left(4;0;1\right),C\left(-10;5;3\right)\). Hãy tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left(ABC\right)\).

Giải:

Với \(A\left(2;-1;3\right),B\left(4;0;1\right),C\left(-10;5;3\right)\) ta có \(\overrightarrow{AB}=\left(2;1;-2\right),\overrightarrow{AC}=\left(-12;6;0\right)\)

Khi đó áp dụng công thức tích vectơ ta được

  \(\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(12;24;24\right)=12\left(1;2;2\right)\)

Như vậy \(\overrightarrow{n}=\left(1;2;2\right)\) là một vectơ pháp tuyến của mặt phẳng \(\left(ABC\right)\).

II. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG

1. Định nghĩa

Phương trình có dạng \(Ax+By+Cz+D=0\), trong đó \(A,B,C\) không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng.

Nhận xét:

a) Nếu mặt phẳng \(\left(\alpha\right)\) có phương trình tổng quát là \(Ax+By+Cz+D=0\) thì nó có một vectơ pháp tuyến là \(\overrightarrow{n}=\left(A;B;C\right)\).

b) Phương trình mặt phẳng đi qua điểm \(M\left(x_0;y_0;z_0\right)\) nhận vectơ \(\overrightarrow{n}\left(A;B;C\right)\) khác \(\overrightarrow{0}\) làm vectơ pháp tuyến là \(A\left(x-x_0\right)+B\left(y-y_0\right)+C\left(z-z_0\right)=0\).

Ví dụ 2: Hãy tìm một vectơ pháp tuyến của mặt phẳng \(\left(\alpha\right)\): \(4x-2y-6z+7=0\).

Giải:

Theo định nghĩa mặt phẳng \(\left(\alpha\right)\): \(4x-2y-6z+7=0\) có một vectơ pháp tuyến có toạ độ là \(\left(4;-2;-6\right)=2\left(2;-1;-3\right)\).

Vậy \(\overrightarrow{n}=\left(2;-1;-3\right)\) là một vectơ pháp tuyến của mặt phẳng \(\left(\alpha\right)\).

Ví dụ 3: Viết phương trình mặt phẳng \(\left(\beta\right)\) có một vectơ pháp tuyến là \(\overrightarrow{b}\left(1;-2;1\right)\) và đi qua điểm \(B\left(0;2;-3\right)\).

Giải:

Phương trình mặt phẳng \(\left(\beta\right)\) có một vectơ pháp tuyến là \(\overrightarrow{b}\left(1;-2;1\right)\) và đi qua điểm \(B\left(0;2;-3\right)\) có dạng: \(1\left(x-0\right)-2\left(y-2\right)+1\left(z-\left(-3\right)\right)=0\) 

hay \(\left(\beta\right)\): \(x-2y+z+7=0\).

2. Các trường hợp riêng

Trong không gian \(Oxyz\) cho mặt phẳng \(\left(\alpha\right)\): \(Ax+By+Cz+D=0\).

a) Nếu \(D=0\): Mặt phẳng \(\left(\alpha\right)\) đi qua gốc toạ độ \(O\).

b) Nếu một trong ba hệ số \(A,B,C\) bằng 0, chẳng hạn \(A=0\) thì mặt phẳng \(\left(\alpha\right)\) song song hoặc chứa trục \(Ox\).

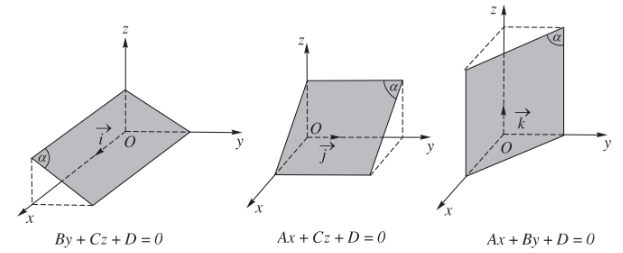
c) Nếu hai trong ba hệ số \(A,B,C\) bằng 0, chẳng hạn \(A=B=0,C\ne0\) thì mặt phẳng \(\left(\alpha\right)\) song song hoặc trùng với mặt phẳng \(\left(Oxy\right)\).

Nhận xét: Nếu cả bốn hệ số \(A,B,C,D\) đều khác 0 thì bằng cách đặt \(a=-\dfrac{D}{A},b=-\dfrac{D}{B},c=-\dfrac{D}{C}\) ta có thể đưa phương trình tổng quát về dạng như sau:

                     \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\).

Phương trình này gọi là phương trình của mặt phẳng theo đoạn chắn.

III. ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC

Trong không gian \(Oxyz\) cho hai mặt phẳng:

               \(\left(\alpha_1\right):A_1x+B_1y+C_1z+D_1=0\) ;

               \(\left(\alpha_2\right):A_2x+B_2y+C_2z+D_2=0\)

Khi đó \(\left(\alpha_1\right)\) và \(\left(\alpha_2\right)\) có hai vectơ pháp tuyến lần lượt là \(\overrightarrow{n_1}\left(A_1;B_1;C_1\right)\) và \(\overrightarrow{n_2}\left(A_2;B_2;C_2\right)\).

1. Điều kiện để hai mặt phẳng song song

Hai mặt phẳng \(\left(\alpha_1\right)\) và \(\left(\alpha_2\right)\) song song hoặc trùng nhau khi và chỉ khi hai vectơ pháp tuyến \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) của chúng cùng phương.

\(\left(\alpha_1\right)\)//\(\left(\alpha_2\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{n_1}=k\overrightarrow{n_2}\\D_1\ne kD_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(A_1;B_1;C_1\right)=k\left(A_2;B_2;C_2\right)\\D_1\ne kD_2\end{matrix}\right.\)

\(\left(\alpha_1\right)\)\(\equiv\)\(\left(\alpha_2\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{n_1}=k\overrightarrow{n_2}\\D_1=kD_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(A_1;B_1;C_1\right)=k\left(A_2;B_2;C_2\right)\\D_1=kD_2\end{matrix}\right.\).

Chú ý: \(\left(\alpha_1\right)\) cắt \(\left(\alpha_2\right)\) \(\Leftrightarrow\overrightarrow{n_1}\ne k\overrightarrow{n_2}\Leftrightarrow\left(A_1;B_1;C_1\right)\ne k\left(A_2;B_2;C_2\right)\).

Ví dụ 4: Viết phương trình mặt phẳng \(\left(\alpha\right)\) đi qua điểm \(M\left(1;-2;3\right)\) và song song với mặt phẳng \(\left(\beta\right):2x-3y+z+5=0\).

Giải:
Do mp\(\left(\alpha\right)\) // mp \(\left(\beta\right)\) nên \(\left(\alpha\right)\) có một vectơ pháp tuyến là \(\overrightarrow{n}\left(2;-3;1\right)\).

Do \(M\left(1;-2;3\right)\in\left(\alpha\right)\) nên phương trình mặt phẳng \(\left(\alpha\right)\) là:

      \(2\left(x-1\right)-3\left(y+2\right)+1\left(z-3\right)=0\) hay \(2x-3y+z-11=0\).

2. Điều kiện để hai mặt phẳng vuông góc

Hai mặt phẳng \(\left(\alpha_1\right)\) và \(\left(\alpha_2\right)\) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến \(\overrightarrow{n_1}\) và \(\overrightarrow{n_2}\) tương ứng của chúng vuông góc với nhau.

\(\left(\alpha_1\right)\perp\left(\alpha_2\right)\Leftrightarrow\overrightarrow{n_1}.\overrightarrow{n_2}=0\Leftrightarrow A_1A_2+B_1B_2+C_1C_2=0\).

Ví dụ 5: Viết phương trình mặt phẳng \(\left(\alpha\right)\) đi qua hai điểm \(A\left(3;1;-1\right)\) và \(B\left(2;-1;4\right)\) và vuông góc với mặt phẳng \(\left(\beta\right):2x-y+3z-1=0\).

Giải:

Ta có \(\overrightarrow{n_{\beta}}\left(2;-1;3\right)\) là vectơ pháp tuyến của mặt phẳng \(\left(\beta\right):2x-y+3z-1=0\)

Hai vectơ không cùng phương có giá song song hoặc nằm trên \(\left(\alpha\right)\) là

    \(\overrightarrow{AB}=\left(-1;-2;5\right)\) và \(\overrightarrow{n_{\beta}}\left(2;-1;3\right)\)

Do đó mặt phẳng \(\left(\alpha\right)\) có vectơ pháp tuyến là \(\overrightarrow{n_{\alpha}}=\left[\overrightarrow{AB},\overrightarrow{n_{\beta}}\right]=\left(-1;13;5\right)\)

Vậy phương trình của \(\left(\alpha\right)\) là 

    \(-1\left(x-3\right)+13\left(y-1\right)+5\left(z+1\right)=0\) hay \(x-13y-5z+5=0\).

IV. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG

Định lí:

Trong không gian \(Oxyz\) cho mặt phẳng \(\left(\alpha\right)\) có phương trình \(Ax+By+Cz+D=0\) và điểm \(M_0\left(x_0;y_0;z_0\right)\). Khoảng cách từ điểm \(M_0\left(x_0;y_0;z_0\right)\) đến mặt phẳng \(\left(\alpha\right)\) kí hiệu là \(d\left(M_0,\left(\alpha\right)\right)\) được tính theo công thức

                           \(d\left(M_0,\left(\alpha\right)\right)=\dfrac{\left|Ax_0+By_0+Cz_0+D\right|}{\sqrt{A^2+B^2+C^2}}\).

Ví dụ 6: Tính khoảng cách từ điểm \(M\left(1;-2;13\right)\) đến mặt phẳng \(\left(\alpha\right):2x-2y-z+3=0\).

Giải:

Áp dụng công thức trên ta có:  \(d\left(M,\left(\alpha\right)\right)=\dfrac{\left|2.1-2.\left(-2\right)-13+3\right|}{\sqrt{2^2+\left(-2\right)^2+\left(-1\right)^2}}=\dfrac{4}{3}\).

Ví dụ 7: Tính khoảng cách giữa hai mặt phẳng song song 

                    \(\left(\alpha\right):x+2y+2x+11=0\)

               và \(\left(\beta\right):x+2y+2x+2=0\).

Giải:

Ta biết khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

Ta lấy \(M\left(0;0;-1\right)\in\left(\beta\right)\), ta có:

            \(d\left(\left(\alpha\right),\left(\beta\right)\right)=d\left(M,\left(\alpha\right)\right)=\dfrac{\left|0+2.0+2.\left(-1\right)+11\right|}{\sqrt{1^2+2^2+2^2}}=\dfrac{9}{3}=3\).