Bài 2: Phép tịnh tiến
Nội dung lý thuyết
I. Phép biến hình
- Định nghĩa:
Quy tắc đặt tương ứng mỗi điểm \(M\) của mặt phẳng với một điểm xác định duy nhất \(M'\) của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
Nếu kí hiệu phép biến hình là \(F\) thì ta viết \(F\left(M\right)=M'\) hay \(M'=F\left(M\right)\) và gọi điểm \(M'\) là ảnh của điểm \(M\) qua phép biến hình \(F\).
Nếu \(H\) là một hình nào đó trong mặt phẳng thì ta kí hiệu \(H'=F\left(H\right)\) là tập các điểm \(M'=F\left(M\right)\), với mọi điểm \(M\) thuộc \(H\). Khi đó ta nói \(F\) biến hình \(H\) thành \(H'\), hay hình \(H'\) là ảnh của của hình \(H\) qua phép biến hình \(F\).
Phép biến hình biến mỗi điểm \(M\) thành chính nó được gọi là phép đồng nhất.
Ví dụ:
Ta đã biết rằng với mỗi điểm \(M\) có một điểm \(M'\) duy nhất là hình chiếu của \(M\) trên đường thẳng \(d\) cho trước. Ta nói điểm \(M'\) là ảnh của điểm \(M\) qua
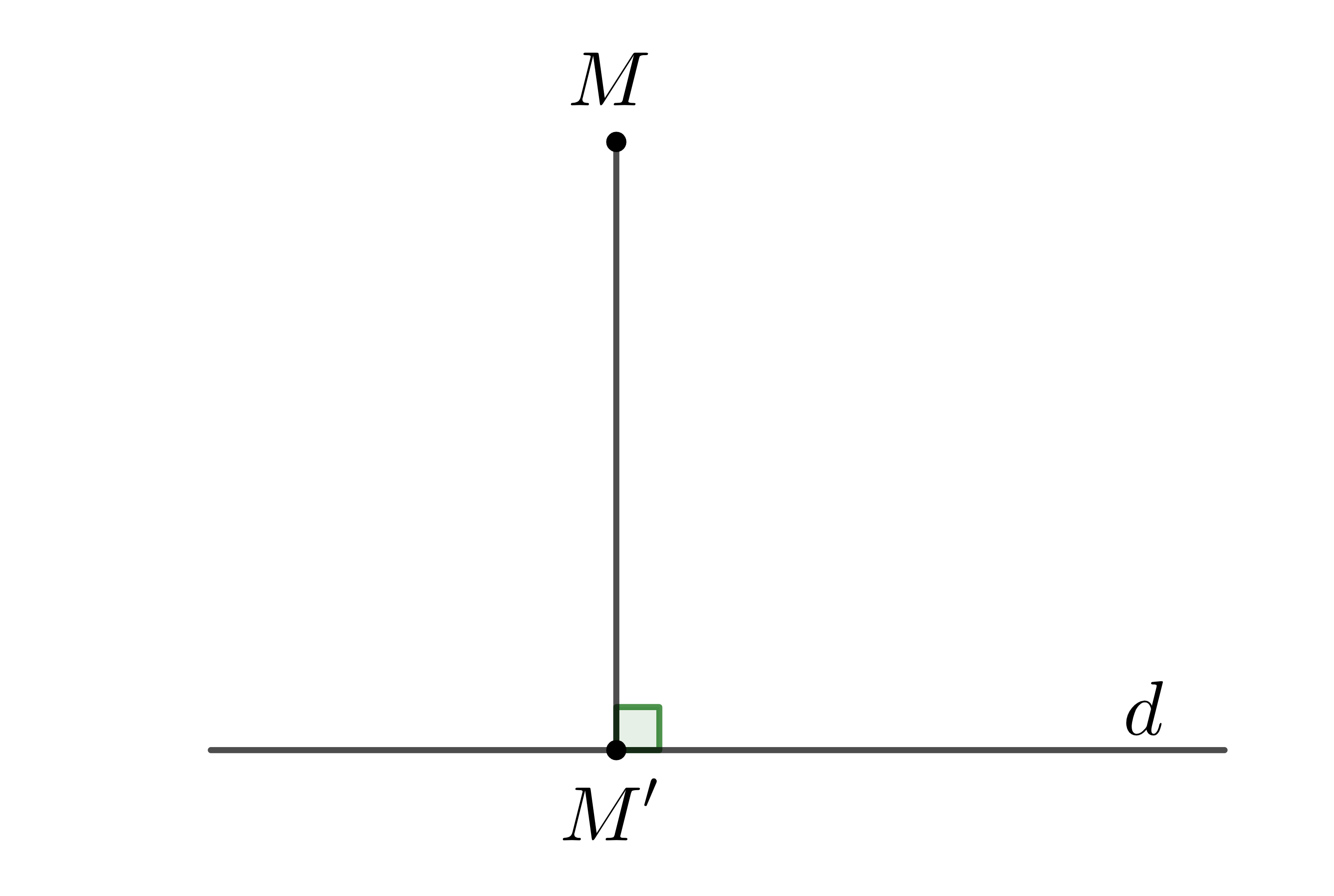
Phản ví dụ: Cho trước một số dương \(a\), với mỗi điểm \(M\) trong mặt phẳng, gọi \(M'\) là điểm sao cho \(MM'=a\). Quy tắc đặt tương ứng điểm \(M\) với điểm \(M'\) nêu trên không phải là phép biến hình vì với mỗi điểm \(M\) có vô số điểm \(M'\) thỏa mãn \(MM'=a\), như vậy điểm \(M'\) không phải xác định duy nhất.
II. Phép tịnh tiến
1. Định nghĩa :
Trong mặt phẳng cho vectơ \(\overrightarrow{v}\) . Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow{MM'}=\overrightarrow{v}\) được gọi là phép tịnh tiến theo vectơ \(\overrightarrow{v}\).
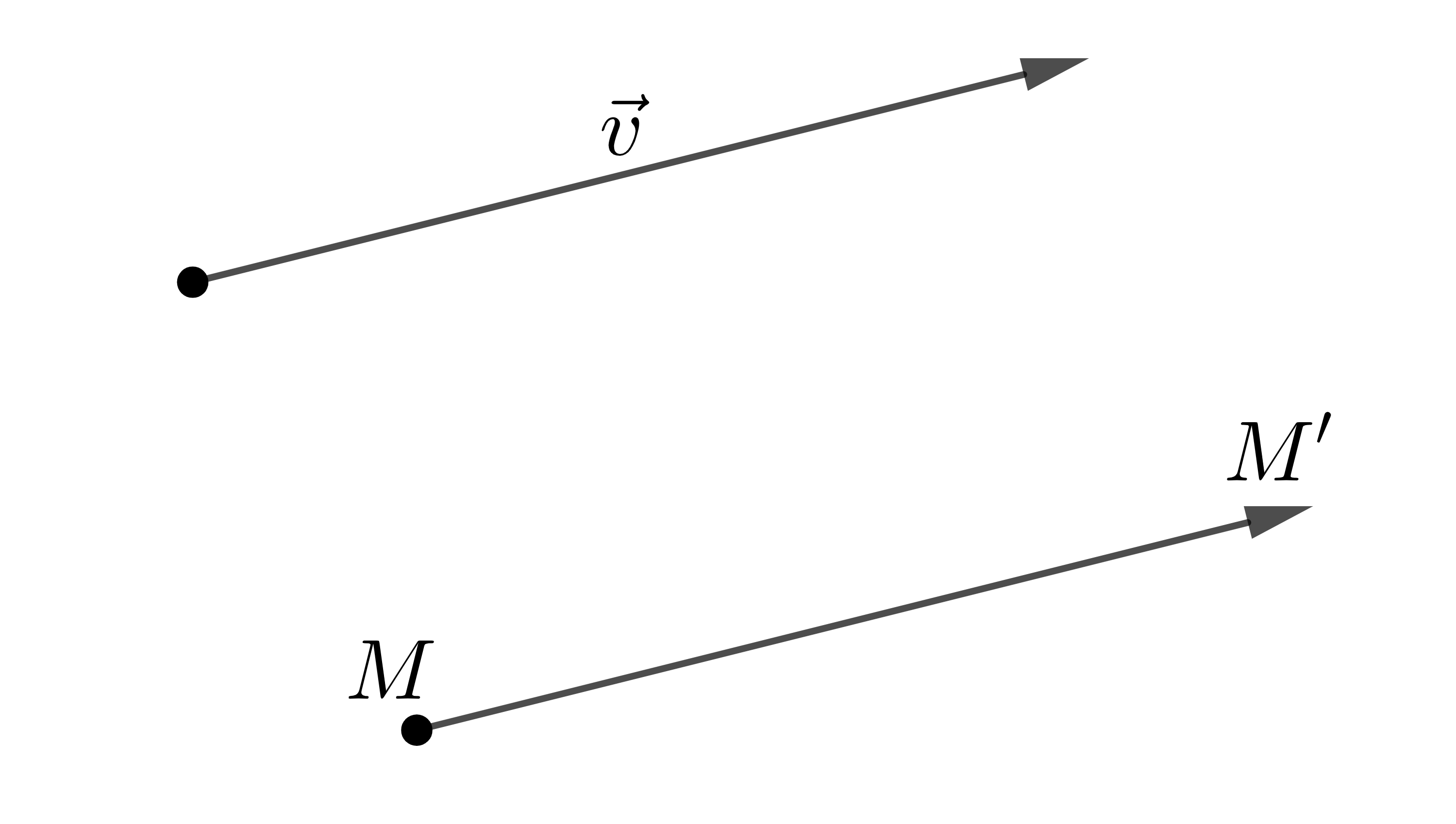
Phép tịnh tiến theo vectơ \(\overrightarrow{v}\) thường được ký hiệu là \(T_{\overrightarrow{v}}\), \(\overrightarrow{v}\) được gọi là vectơ tịnh tiến.
Như vậy:
\(T_{\overrightarrow{v}}\left(M\right)=M'\Leftrightarrow\overrightarrow{MM'}=\overrightarrow{v}\)
Phép tịnh tiến theo vectơ - không chính là phép đồng nhất.
Ta dễ dàng nhận thấy phép tịnh tiến là một phép biến hình.
Ví dụ:
a) Phép tịnh tiến \(T_{\overrightarrow{u}}\) biến các điểm \(A,B,C\) tương ứng thành các điểm \(A',B',C'\):
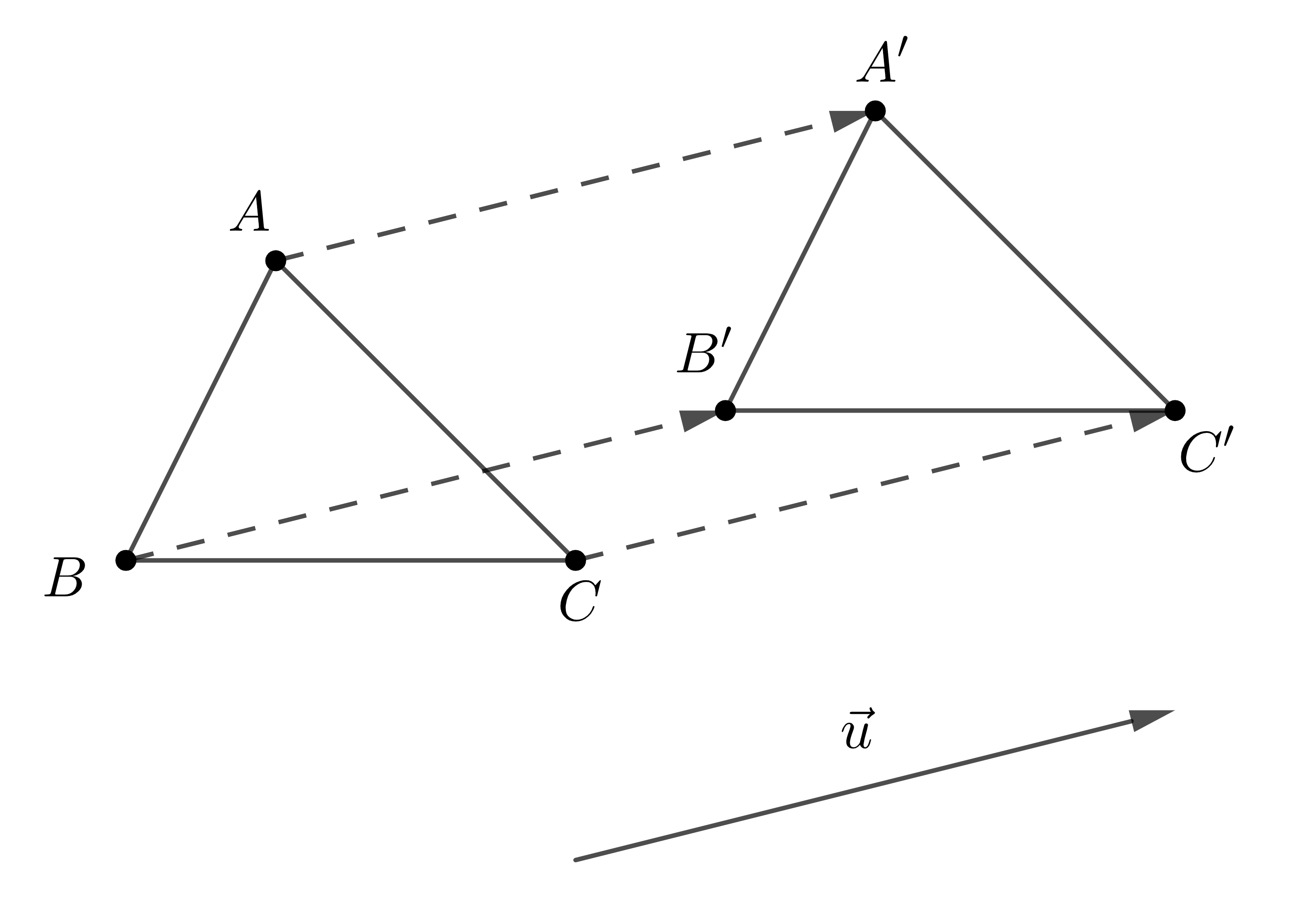
b) Phép tịnh tiến \(T_{\overrightarrow{v}}\) biến hình \(H\) thành hình \(H'\):
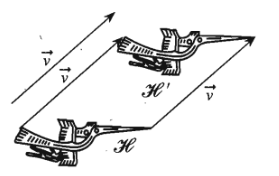
2.Các tính chất của phép tịnh tiến
a) Tính chất 1:
Nếu \(T_{\overrightarrow{v}}\left(M\right)=M'\), \(T_{\overrightarrow{v}}\left(N\right)=N'\) thì \(\overrightarrow{M'N'}=\overrightarrow{MN}\) và từ đó suy ra \(M'N'=MN\).
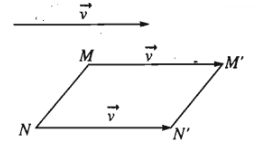
Thật vậy, ta có \(\overrightarrow{MM'}=\overrightarrow{NN'}=\overrightarrow{v}\) và \(\overrightarrow{M'M}=-\overrightarrow{v}\), do đó:
\(\overrightarrow{M'N'}=\overrightarrow{M'M}+\overrightarrow{MN}+\overrightarrow{NN'}=-\overrightarrow{v}+\overrightarrow{MN}+\overrightarrow{v}=\overrightarrow{MN}\)
Từ đó suy ra \(M'N'=MN\).
Nói cách khác, phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
Ví dụ 1: Cho hai điểm \(A\left(1;2\right)\), \(B\left(2;4\right)\) và vectơ \(\overrightarrow{u}=\left(2;\dfrac{1}{2}\right)\). Gọi \(A',B'\) lần lượt là ảnh của hai điểm \(A,B\) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}\). Tính độ dài \(A'B'\).
Giải:
Ta có: \(A\left(1;2\right)\), \(B\left(2;4\right)\) \(\Rightarrow AB=\sqrt{\left(2-1\right)^2+\left(4-2\right)^2}=\sqrt{5}\)
Theo tính chất trên \(A'B'=AB\) nên \(A'B'=\sqrt{5}\).
@2093703@
b) Tính chất 2:
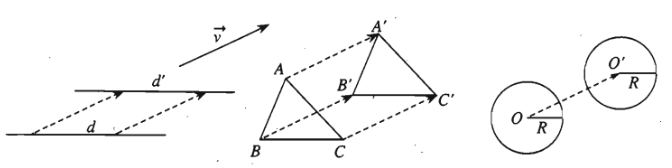
Phép tịnh tiến biến đường thẳng thành đường thằng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
@61684@
3. Biểu thức tọa độ của phép tịnh tiến
- Trong mặt phẳng \(Oxy\) cho vectơ \(\overrightarrow{v}\left(a;b\right)\) và một điểm \(M\left(x;y\right)\) . Phép tịnh tiến theo vectơ \(\overrightarrow{v}\) biến điểm \(M\) thành điểm \(M'\left(x';y'\right)\) thì \(M'\left(x';y'\right)\) có tọa độ là \(\begin{cases}x'=a+x\\y'=b+y\end{cases}\).
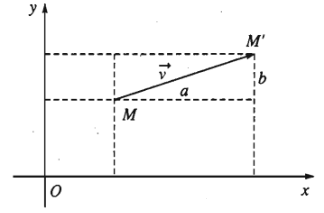
Biểu thức trên được gọi là biểu thức toạ độ của phép tịnh tiến \(T_{\overrightarrow{v}}\).
Ví dụ 2: Cho điểm \(M\left(3;4\right)\) và vectơ \(\overrightarrow{v}=\left(\dfrac{1}{2};1\right)\). Tìm toạ độ của điểm \(M'\) là ảnh của \(M\left(3;4\right)\) qua phép tịnh tiến \(T_{\overrightarrow{v}}\).
Giải:
Toạ độ của điểm \(M'\) là ảnh của \(M\left(3;4\right)\) qua phép tịnh tiến \(T_{\overrightarrow{v}}\) được tính bởi: \(\left\{{}\begin{matrix}x_{M'}=3+\dfrac{1}{2}=\dfrac{7}{2}\\y_{M'}=4+1=5\end{matrix}\right.\)
Vậy ta xác định được toạ độ điểm \(M'\) là \(M'\left(\dfrac{7}{2};5\right)\).
@61677@
Ví dụ 3: Cho đường thẳng \(\left(d\right):x-2y+3=0\) và vectơ \(\overrightarrow{v}=\left(-1;2\right)\). Viết phương trình đường thẳng \(\left(d'\right)\) là ảnh của đường thẳng \(\left(d\right)\) qua phép tịnh tiến theo vectơ \(\overrightarrow{v}=\left(-1;2\right)\).
Giải:
Đường thẳng \(\left(d\right)\) có vectơ pháp tuyến \(\overrightarrow{n_d}=\left(1;-2\right)\) nên vectơ chỉ phương là \(\overrightarrow{u_d}=\left(2;1\right)\).
\(\Rightarrow\overrightarrow{v}\) không cùng phương với vectơ chỉ phương của \(\left(d\right)\)
Do đó phép tịnh tiến \(\overrightarrow{v}\) biến đường thẳng \(\left(d\right)\) thành đường thẳng \(\left(d'\right)\) song song với \(\left(d\right)\)
Nên đường thẳng \(\left(d'\right)\) có dạng \(x-2y+m=0\).
Chọn điểm \(M\left(-1;1\right)\in\left(d\right)\)
Ảnh của \(M\) qua phép tịnh tiến theo vectơ \(\overrightarrow{v}\) là \(M'\left(-2;3\right)\in\left(d'\right)\).
Khi đó ta có: \(\left(-2\right)-2.3+m=0\Leftrightarrow m=8\)
Vậy phương trình đường thẳng \(\left(d'\right)\) là \(x-2y+8=0\).
Ví dụ 4: Cho đường tròn \(\left(C'\right):\left(x-1\right)^2+\left(y-2\right)^2=9\) và \(\overrightarrow{v}\left(2;3\right)\). Viết phương trình đường tròn \(\left(C\right)\) biết \(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\).
Giải:
Đường tròn \(\left(C'\right):\left(x-1\right)^2+\left(y-2\right)^2=9\) có tâm \(I'\left(1;2\right)\), bán kinh \(R=3\)
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\left(C\right)\).
Do \(T_{\overrightarrow{v}}\left(\left(C\right)\right)=\left(C'\right)\) nên \(T_{\overrightarrow{v}}\left(I\right)=I'\) \(\Rightarrow\left\{{}\begin{matrix}1=x+2\\2=y+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=-1\end{matrix}\right.\) \(\Rightarrow\) \(I\left(-1;-1\right)\)
Như vậy đường tròn \(\left(C\right)\) có tâm \(I\left(-1;-1\right)\) và bán kính \(R=3\)
Nên \(\left(C\right)\): \(\left(x+1\right)^2+\left(y+1\right)^2=9\).