Bài 11: Hình chiếu trục đo
Nội dung lý thuyết
I. NỘI DUNG CỦA PHƯƠNG PHÁP HÌNH CHIẾU TRỤC ĐO
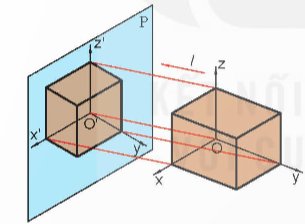
Hình chiếu trục đo được xây dựng như sau:
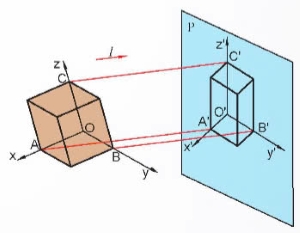
- Gắn hệ trục toạ độ Oxyz vào vật thể, với các trục toạ độ đặt theo ba chiều dài, rộng và cao của vật thể.
+ Chiếu vật thể cùng hệ trục toạ độ theo hướng l lên mặt phẳng hình chiếu P ( l không song song P và không song song với mặt phẳng toạ độ nào).
+ Kết quả trên mặt phẳng P nhận được một hình chiếu của vật thể và hệ toạ độ O'x'y'z'.
+ Hình chiếu đó gọi là hình chiếu trục đo (HCTĐ) của vật thể.
- Các trục O'x', O'y' và O'z' gọi là các trục đo.
+ Góc giữa các trục đo \(\widehat{x'O'y'}\), \(\widehat{y'O'z'}\), \(\widehat{z'O'x'}\) gọi là các góc trục đo.
- Hệ số biến dạng là tỉ số độ dài hình chiếu một đoạn thẳng song song hoặc nằm trên trục toạ độ với độ dài thực tế của đoạn thẳng đó.
- Theo từng trục toạ độ, có các hệ số biến dạng như sau:
+ \(p=\dfrac{O'A'}{OA}\) là hệ số biến dạng theo trục O'x'.
+ \(q=\dfrac{O'B'}{OB}\) là hệ số biến dạng theo trục O'y'.
+ \(r=\dfrac{O'C'}{OC}\) là hệ số biến dạng theo trục O'z'.
II. HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU
Trong hình chiếu trục đo vuông góc đều, phương chiếu l vuông góc với mặt phẳng hình chiếu P và các trục toạ độ Ox, Oy, Oz làm với mặt phẳng hình chiếu P các góc bằng nhau.
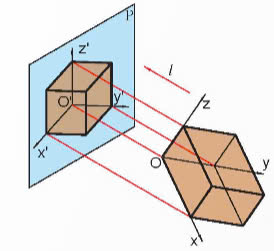
- Góc trục đo \(\widehat{x'O'y'}\) = \(\widehat{y'O'z'}\) = \(\widehat{z'O'x'}\) = 120°.
- Hệ số biến dạng \(p=q=r\approx0,82\). Để thuận tiện cho việc dụng hình, quy ước lấy q = p = r = 1.
- Hình chiếu trục đo của hình tròn:
+ Hình chiếu trục đo vuông góc đều của những hình tròn nằm trên các mặt phẳng song song với các mặt phẳng toạ độ là các hình elip có phương của trục dài khác nhau.
III. HÌNH CHIẾU TRỤC ĐO XIÊN GÓC CÂN
- Trong hình chiếu trục đo xiên góc cân, mặt phẳng tọa độ xOz song song với mặt phẳng hình chiếu P, l không vuông góc với P.
- Góc trục đo \(\widehat{x'O'y}\) = \(\widehat{y'O'z'}\) = 135°, \(\widehat{x'O'z'}\) = 90°.
- Hệ số biến dạng p = r = 1, q = 0,5.
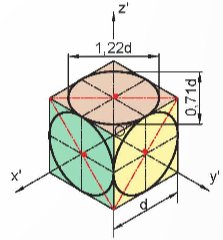
- Hình chiếu trục đo xiên góc cân của một hình lập phương có các hình tròn nội tiếp trong các mặt.
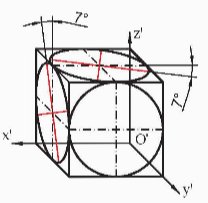
- Hình chiếu trục đo của hình tròn nằm trên mặt phẳng song song với mặt phẳng toạ độ xOz là hình tròn.
- Hình tròn nằm trên mặt phẳng song song với mặt toạ độ xOy hoặc yOz có hình chiếu trục đo là elip.
- Trục dài của elip bằng 1,06d, trục ngắn bằng 0,33d (d là đường kính của đường tròn).
- Trục dài của elip làm với trục nằm ngang hoặc trục thẳng đứng một góc 7°.
IV. VẼ HÌNH CHIẾU TRỤC ĐO
1. Vẽ hình chiếu trục đo của một điểm
- Một điểm A có hình chiếu đứng là A1, hình chiếu bằng A2 thì điểm A có các toạ độ xA, yA, zA.
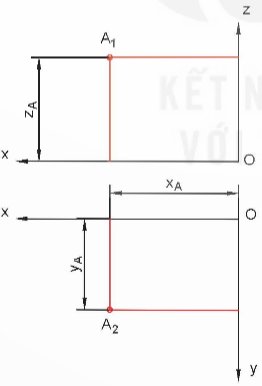
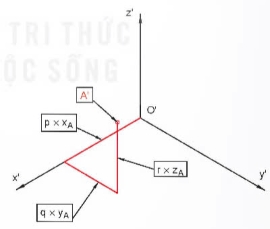
- Hình chiếu trục đo của điểm A là điểm A' có các toạ độ trục đo là x'A', y'A', z'A' với x'A' = p \(\times\) xA, y'A' = q \(\times\) yA, z'A' = r \(\times\) zA.
2. Vẽ hình chiếu trục đo của vật thể
- Bước 1. Gắn hệ trục toạ độ Oxyz vào vật thể:
+ Từ các hình chiếu vuông góc đã cho, phác hoạ hình dáng không gian của vật thể.
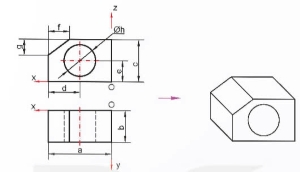
- Bước 2. Vẽ hình chiếu trục đo của hình hộp bao ngoài vật thể có kích thước:
+ Dài a, rộng b và cao c đặt lên ba trục đo theo hệ số biến dạng của chúng.
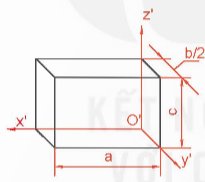
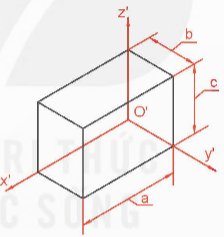
- Bước 3: Vẽ các thành phần của vật thể.
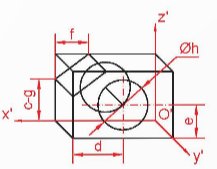
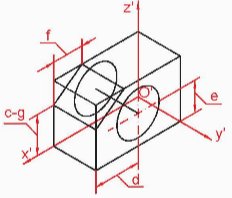
- Bước 4: Tẩy các đường nét phụ, đường khuất, tô đậm các cạnh thấy.