Bài 1: Vectơ trong không gian

I. ĐỊNH NGHĨA VÀ CÁC PHÉP TOÁN VỀ VECTƠ TRONG KHÔNG GIAN

Cho đoạn thẳng \(AB\) trong không gian. Nếu ta chọn điểm đầu là \(A\), điểm cuối là \(B\) ta có một vectơ, kí hiệu là \(\overrightarrow{AB}\).

1. Định nghĩa

Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu \(\overrightarrow{AB}\) chỉ vectơ có điểm đầu là \(A\), điểm cuối là \(B\). Vectơ còn được kí hiệu là \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y}\),...

Các khái niệm liên qua như giá của vectơ, độ dài của vectơ, vectơ cùng phương, cùng hướng, vectơ - không, sự bằng nhau của hai vectơ,... được định nghĩa tương tự như trong mặt phẳng.

2. Phép cộng và phép trừ vectơ trong không gian

Phép cộng và phép trừ vectơ trong không gian được định nghĩa tương tự như phép cộng và phép trừ vectơ trong mặt phẳng. Phép cộng vectơ trong không gian cũng có những tính chất tương tự như phép cộng vectơ trong mặt phẳng. Ta vẫn có thể áp dụng các quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong mặt phẳng.

Ví dụ 1: Cho tứ diện \(ABCD\). Chứng minh rằng: \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}\).

Giải:

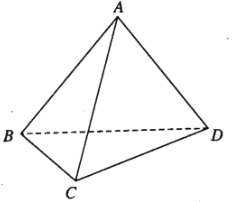
Theo quy tắc ba điểm ta có: \(\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}\)

Do đó: \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BD}=\overrightarrow{AD}+\left(\overrightarrow{BD}+\overrightarrow{DC}\right)=\overrightarrow{AD}+\overrightarrow{BC}\).

Quy tắc hình hộp:

Cho hình hộp \(ABCD.A'B'C'D'\) có ba cạnh xuất phát từ đỉnh \(A\) là \(AB,AD,AA'\) và có đường chéo là \(AC'\). Khi đó ta có quy tắc hình hộp là:

                      \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)

3. Phép nhân vectơ với một số

Trong không gian, tích của vectơ \(\overrightarrow{a}\) với một số \(k\ne0\) là vectơ \(k\overrightarrow{a}\) được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng.

Ví dụ 2: Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AD,BC\) và \(G\) là trọng tâm của tam giác \(BCD\). Chứng minh rằng:

    a) \(\overrightarrow{MN}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{DC}\right)\) ;

    b) \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}\).

Giải:

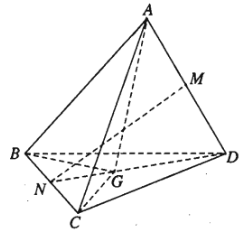
a) Ta có: \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}\) và \(\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{CN}\)

Do đó: \(2.\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BN}+\overrightarrow{CN}\)

Vì \(M\) là trung điểm của \(AD\) nên \(\overrightarrow{MA}+\overrightarrow{MD}=\overrightarrow{0}\) và \(N\) là trung điểm của \(BC\) nên \(\overrightarrow{BN}+\overrightarrow{CN}=\overrightarrow{0}\).

Do đó \(2.\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{DC}\) suy ra \(\overrightarrow{MN}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{DC}\right)\).

b) Ta có: \(\overrightarrow{AB}=\overrightarrow{AG}+\overrightarrow{GB}\) ; \(\overrightarrow{AC}=\overrightarrow{AG}+\overrightarrow{GC}\) ; \(\overrightarrow{AD}=\overrightarrow{AG}+\overrightarrow{GD}\)

Suy ra \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\)

Vì \(G\) là trọng tâm tam giác \(BCD\) nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)

Do đó \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}\).

II. ĐIỀU KIỆN ĐỒNG PHẲNG CỦA BA VECTƠ

1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian

Trong không gian cho ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đều khác vectơ - không. Nếu từ một điểm \(O\) bất kì vẽ \(\overrightarrow{OA}=\overrightarrow{a}\), \(\overrightarrow{OB}=\overrightarrow{b}\), \(\overrightarrow{OC}=\overrightarrow{c}\) thì có thể xảy ra hai trường hợp:

+) Trường hợp các đường thẳng \(OA,OB,OC\) không cùng nằm trong một mặt phẳng, khi đó ta nói ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) không đồng phẳng.

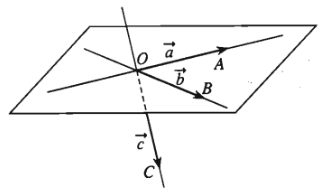
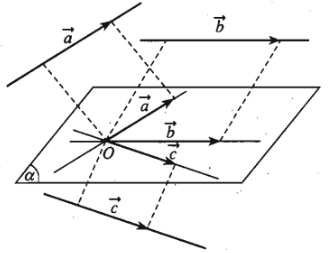
+) Trường hợp các đường thẳng \(OA,OB,OC\) cùng nằm trong một mặt phẳng thì ta nói ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đồng phẳng.

Trong trường hợp này giá của các vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) luôn song song với một mặt phẳng.

Chú ý: Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên không phụ thuộc vào việc chọn điểm \(O\).

2. Định nghĩa

Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

3. Điều kiện để ba vectơ đồng phẳng

- Định lí 1:

Trong không gian cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) không cùng phương và vectơ \(\overrightarrow{c}\). Khi đó ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) đồng phẳng khi và chỉ khi có cặp số \(m,n\) sao cho \(\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\). Ngoài ra cặp số \(m,n\) là duy nhất.

Ví dụ 3: Cho tứ diện \(ABCD\). Gọi \(M,N\) là trung điểm \(AB,CD\). Trên các cạnh \(AD\) và \(BC\)lần lượt lấy các điểm \(P,Q\) sao cho \(\overrightarrow{AP}=\dfrac{2}{3}\overrightarrow{AD}\) và \(\overrightarrow{BQ}=\dfrac{2}{3}\overrightarrow{BC}\). Chứng minh rằng bốn điểm \(M,N,P,Q\) cùng thuộc một mặt phẳng.

Giải:

 Ta có \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\)  và \(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)

Nên \(2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{BC}\) suy ra \(\overrightarrow{MN}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{BC}\right)\) (1)

Mặt khác vì \(\overrightarrow{AP}=\dfrac{2}{3}\overrightarrow{AD}\) nên \(\overrightarrow{AD}=\dfrac{3}{2}\overrightarrow{AP}\) ; \(\overrightarrow{BQ}=\dfrac{2}{3}\overrightarrow{BC}\) nên \(\overrightarrow{BC}=\dfrac{3}{2}\overrightarrow{BQ}\)

Do đó từ (1) suy ra \(\overrightarrow{MN}=\dfrac{1}{2}.\dfrac{3}{2}\left(\overrightarrow{AP}+\overrightarrow{BQ}\right)=\dfrac{3}{4}\left(\overrightarrow{AM}+\overrightarrow{MP}+\overrightarrow{BM}+\overrightarrow{MQ}\right)\)

mà \(\overrightarrow{AM}+\overrightarrow{BM}=\overrightarrow{0}\) nên \(\overrightarrow{MN}=\dfrac{3}{4}\left(\overrightarrow{MP}+\overrightarrow{MQ}\right)=\dfrac{3}{4}\overrightarrow{MP}+\dfrac{3}{4}\overrightarrow{MQ}\)

Vậy các điểm \(M,N,P,Q\) cùng thuộc một mặt phẳng.

- Định lí 2:

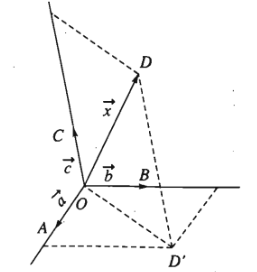
Trong không gian cho ba vectơ không đồng phẳng \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\). Khi đó với mọi vectơ \(\overrightarrow{x}\) ta đều tìm được một bộ ba số \(m,n,p\) sao cho \(\overrightarrow{x}=m\overrightarrow{a}+n\overrightarrow{b}+p\overrightarrow{c}\). Ngoài ra bộ ba số \(m,n,p\) là duy nhất.

Ví dụ 4: Cho hình hộp \(ABCD.EFGH\) có \(\overrightarrow{AB}=\overrightarrow{a}\), \(\overrightarrow{AD}=\overrightarrow{b}\), \(\overrightarrow{AE}=\overrightarrow{c}\). Gọi \(I\) là trung điểm đoạn \(BG\). Hãy biểu thị vectơ \(\overrightarrow{AI}\) qua ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\).

Giải:

Vì \(I\) là trung điểm \(BG\) nên \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AG}\right)\)

trong đó \(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AE}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)

Vậy \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{a}+\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right)\) suy ra \(\overrightarrow{AI}=\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{b}+\dfrac{1}{2}\overrightarrow{c}\).