Bài 1. Tập hợp Q các số hữu tỉ
Nội dung lý thuyết
I. Số hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số \(\dfrac{a}{b}\) với \(a,b\in \mathbb Z, b\ne 0\).
Tập hợp số hữu tỉ được kí hiệu là \(\mathbb Q\).
Ví dụ 1: Các số -7; 0; -0,75 và \(1\dfrac{1}{2}\) đều là các số hữu tỉ vì đều viết được dưới dạng phân số.
Chú ý:
+ Mọi số nguyên là một số hữu tỉ.
+ Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ.
@7285245@
II. Biểu diễn số hữu tỉ trên trục số
Tương tự đối với số nguyên, ta có thể biểu diễn mọi số hữu tỉ trên trục số.
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số, ta có thể chọn một trong những phân số đó để biểu diễn số hữu tỉ trên trục số. Thông thường, ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.
Ví dụ 2: Biểu diễn số hữu tỉ \(\dfrac{9}{10}\) trên trục số.
Hướng dẫn giải
Để biểu diễn số hữu tỉ \(\dfrac{9}{10}\) ta làm như sau:
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 10 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{10}\) đơn vị cũ).
+ Đi theo chiều dương của trục số, bắt đầu từ điểm 0 ta lấy 9 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỷ \(\dfrac{9}{10}\).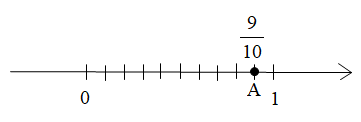
@7285317@
III. Số đối của một số hữu tỉ
+ Trên trục số, hai số hữu tỉ (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.
+ Số đối của số hữu tỉ a kí hiệu là -a.
+ Số đối của số 0 là 0.
Nhận xét: Số đối của số -a là số a tức là -(-a) = a.
Ví dụ 3: Tìm số đối của -3 và \(\dfrac{-7}{5}\).
Hướng dẫn giải
Số đối của -3 là 3.
Số đối của \(\dfrac{-7}{5}\) là \(\dfrac{7}{5}.\)
@7285394@
IV. So sánh các số hữu tỉ
1. So sánh hai số hữu tỉ
Cũng như số nguyên, trong hai số hữu tỉ khác nhau luôn có một số nhỏ hơn số kia.
+ Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a.
+ Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
+ Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.
+ Số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
+ Nếu a < b và b < c thì a < c.
2. Cách so sánh hai số hữu tỉ.
Nhận xét:
+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta so sánh chúng theo những quy tắc đã biết ở lớp 6.
+ Ngoài hai trường hợp trên, để so sánh hai số hữu tỉ, ta viết chúng về cùng dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.
Ví dụ 4: So sánh
a) \(-0,125\) và \(\dfrac{-1}{5}\); b) \(\dfrac{-4}{3}\) và -0,75.
Hướng dẫn giải
a) Ta có \(\dfrac{-1}{5}\) = -0,2.
Do -0,125 > -0,2 nên -0,125 > \(\dfrac{-1}{5}\).
b) Ta có -0,75 = \(\dfrac{-3}{4}\) = \(\dfrac{-9}{12}\);
\(\dfrac{-4}{3}=\dfrac{-16}{12}\).
Do \(\dfrac{-9}{12}\) > \(\dfrac{-16}{12}\) nên -0,75 > \(\dfrac{-4}{3}.\)
@7285449@
3. Minh họa trên trục số
Giả sử hai điểm x và y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số nằm ngang. Khi so sánh hai số hữu tỉ, ta viết chúng ở dạng phân số có cùng mẫu số dương rồi so sánh tử số, tức là so sánh hai số nguyên. Vì vậy, cũng như số nguyên, nếu x < y hay y > x thì x nằm bên trái điểm y. Tương tự, nếu x < y hay y > x thì x nằm phía dưới điểm y trên trục số thẳng đứng.
Ví dụ 5: Sắp xếp các số \(-1; -3; \dfrac{-3}{4}\) theo thứ tự tăng dần.
Hướng dẫn giải
Ta có
\(-1=\dfrac{-4}{4}\\ -3=\dfrac{-12}{4}\)
Mà \(\dfrac{-3}{4}>\dfrac{-4}{4}>\dfrac{-12}{4}\) nên \(\dfrac{-3}{4}>-1>-3.\)
Vậy các số đã cho được sắp xếp theo thứ tự tăng dần là -3; -1; \(\dfrac{-3}{4}\).
@7285580@