Cho tam giác ABC vuông tại C biết CB = 8cm , AB = 10cm
a) Tính AC
b) Trên AB lấy điểm D sao cho AD = 6 cm . C/m : tam giác ACD cân
c) Tia phân giác góc A cắt CD và CB tại I và K . C/m : AI vuông góc với CD
d) So sánh độ dài KC và KB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Biết AC = 8cm BC=10cm
a) Tính AB, so sánh các góc của tam giác ABC
b) Trên tia đối tia AB lấy điểm D sao cho AD=AB. Đường thẳng qua A song song BC cắt DC tại N. Chứng minh tam giác ACB = tam giác ACD và tam giác ANC cân
c) Trên đoạn AC lấy điểm G sao cho GA = 1/2 GC. Chứng minh B;G;n thẳng hàng
a: \(AB=\sqrt{BC^2-AC^2}=6\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
Đúng 0
Bình luận (0)
1)Cho tam giác ABC vuông tại A. Các tia phân giác của góc B và C cắt nhau ở I. Kẻ IH vuông góc với BC(H thuộc BC). Biết HI1cm, HB2cm, HC3cm. Tính chu vi tam giác ABC2) Cho tam giác ABC có góc B lớn hơn góc C, đường phân giác AD. Gọi H là chân đường vuông kẻ từ A đến BC. Chứng minh rằng góc HAD bằng nửa hiệu của hai góc B và góc C.3)Cho tam giác ABC vuông tại A. Lấy điểm D trên cạnh AB sao cho góc ACD1/3 góc ACB. Lấy điểm E trên cạnh AC sao cho ABE1/3 góc ACB. BE và CD cắt nhau tại O. Gọi k là g...
Đọc tiếp
1)Cho tam giác ABC vuông tại A. Các tia phân giác của góc B và C cắt nhau ở I. Kẻ IH vuông góc với BC(H thuộc BC). Biết HI=1cm, HB=2cm, HC=3cm. Tính chu vi tam giác ABC
2) Cho tam giác ABC có góc B lớn hơn góc C, đường phân giác AD. Gọi H là chân đường vuông kẻ từ A đến BC. Chứng minh rằng góc HAD bằng nửa hiệu của hai góc B và góc C.
3)Cho tam giác ABC vuông tại A. Lấy điểm D trên cạnh AB sao cho góc ACD=1/3 góc ACB. Lấy điểm E trên cạnh AC sao cho ABE=1/3 góc ACB. BE và CD cắt nhau tại O. Gọi k là giao điểm các đương phân giác của tam giác OBC. Tam giác DEK là tam giác gì?
4) Tam giác ABC có góc A bằng 100 độ. Gọi CD là tia đối của tia CB. Tia phân giác của góc B cắt tia phân giác của góc ACD tại K. Tính số đo góc BAK
Câu 12: Cho tam giác ABC vuông tại C , có AB = 10 cm, AC cm = 6 . Trên tia đối của tia CB lấy D sao cho CD=CB .
a) Tính BC , so sánh góc A và góc B của tam giác ABC
b) Chứng minh tam giác ABD cân tại A.
c) Gọi M là trung điểm của AD , BM cắt AC tại G. Chứng minh GB +2GC>AB
d) Qua C kẻ CN DA / / sao cho N thuộc AB . Chứng minh D, G ,N thẳng hàng .
a: BC=8cm
BC>AC
=>góc A>góc B
b: XétΔABD có
AC vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
c: GB+2GC=GB+GA>AB
Đúng 0
Bình luận (0)
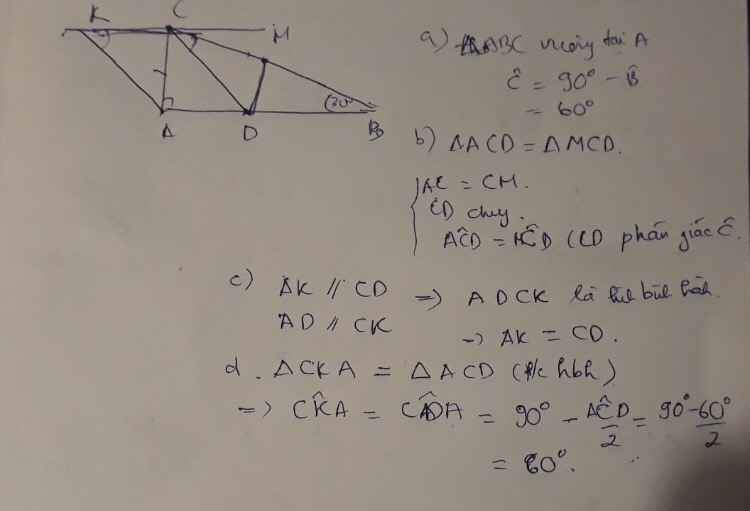
cho tam giác ABC vuông tại A có góc B=30⁰
a) tính góc C
b) vẽ tia phân giác của góc cắt cạnh AB tại D
c) Trên cạnh CB lấy điểm M sao cho CM=CA. CM tam giác ACD = tam giác MCD
d) Qua C vẽ đường thẳng xy vuông góc với CA. Từ A kẻ đường thẳng song song với CD cắt xy ở K. CM: AK=CD
e) tính góc AKC
Cho tam giác ABC có AB = 4 cm, AC = 3 cm, BC = 5 cm.
a) Chứng minh : tam giác ABC vuông
b) Trên AB lấy D sao cho AD = 3 cm. Chứng minh góc ACD = góc ADC
c) Tia phân giác góc CAD cắt BC tại M. So sánh MC và MD ?
d) Cho AM cắt CD tại K. Chứng minh AK < \(\frac{CB}{2}\)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. Trên tia AH lấy D sao cho H là trung điểm của AD. Gọi AB cắt CD tại E; BD cắt AC tại K. Chứng minh:
a) Tam giác ACD cân
b) Tam giác ABC = tam giác DBC và KD vuông góc CE
c) Tam giác CEK cân
d)CB vuông góc KE và AD//EK
a) Xét ΔCAH vuông tại H và ΔCDH vuông tại H có
CH chung
AH=DH(gt)
Do đó: ΔCAH=ΔCDH(hai cạnh tương ứng)
Suy ra: CA=CD(Hai cạnh tương ứng)
Xét ΔCAD có CA=CD(cmt)
nên ΔCAD cân tại C(Định nghĩa tam giác cân)
b) Xét ΔBAH vuông tại H và ΔBDH vuông tại H có
BH chung
AH=DH(gt)
Do đó: ΔBAH=ΔBDH(hai cạnh góc vuông)
Suy ra: BA=BD(Hai cạnh tương ứng)
Xét ΔABC và ΔDBC có
CA=CD(cmt)
BC chung
AB=DB(cmt)
Do đó: ΔABC=ΔDBC(c-c-c)
Suy ra: \(\widehat{BAC}=\widehat{BDC}\)(hai góc tương ứng)
mà \(\widehat{BAC}=90^0\)(gt)
nên \(\widehat{BDC}=90^0\)
hay KD\(\perp\)CE(đpcm)
Đúng 1
Bình luận (0)
c) Xét ΔCAE vuông tại A và ΔCDK vuông tại D có
CA=CD(cmt)
\(\widehat{ACE}=\widehat{DCK}\)(hai góc đối đỉnh)
Do đó: ΔCAE=ΔCDK(cạnh góc vuông-góc nhọn kề)
Suy ra: CE=CK(hai cạnh tương ứng)
Xét ΔCEK có CE=CK(cmt)
nên ΔCEK cân tại C(Định nghĩa tam giác cân)
d) Ta có: ΔCAE=ΔCDK(cmt)
nên AE=DK(hai cạnh tương ứng)
Ta có: BA+AE=BE(A nằm giữa B và E)
BD+DK=BK(D nằm giữa B và K)
mà BA=BD(cmt)
và AE=DK(cmt)
nên BE=BK
Ta có: CE=CK(cmt)
nên C nằm trên đường trung trực của EK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BE=BK(cmt)
nên B nằm trên đường trung trực của EK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BC là đường trung trực của EK
hay BC\(\perp\)EK
mà BC\(\perp\)AD(cmt)
nên AD//EK(Định lí 1 từ vuông góc tới song song)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B = 30 độ .
a) Tính góc C
b) vẽ tia phân giác của góc C cắt cạnh AB tại D . Trên cạnh CB lấy điểm M sao cho CM = CA . CMR : tam giác ACD = tam giác MCD .
Qua C vẽ đường thẳng xy vuông góc CA . Từ A kẻ đường thẳng // vs CD cắt xy ở K . Cm : AK = CD
c) tính góc AKC
mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!
Đúng 2
Bình luận (0)
a) Ta có : A=900 ; B=300
=> C=180-A-B=180-90-30=60
b) Xét tam giác ACD và MCD ta có :
CD chung (1)
CM=CA (gt)(2)
góc ACD=góc DCM (gt) (3)
Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)
c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành
=>AK=CD (cặp cạnh tương ứng )
d)Ta có : \(\widehat{BDC}\)=180-30-60:2=1200
\(\widehat{CPA}\)=180-120=60
Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại C, góc B = 2 góc A
a) Tính góc A và góc B
b) Trên tia đối tia CB lấy điểm D sao cho CD = CB. CM AD = AB
c) Trên AD lấy điểm M, trên AB lấy điểm N sao cho AM = AN . Cm : CM = CN
d) Gọi I là giao điểm của AC và MN . Cm : IM = IN
Cho tam giác ABC vuông tại A có AC> AB. Đường cao AH. Trên tia HC lấy D sao cho HD=HB. Kẻ CE vuông góc AD. C/M
a) tam giác AHB = tam giác AHD ; góc BAH = góc ACB
b) CB là phân giác của góc ACE
c) Gọi giao điểm của AH và CE là K. C/M: KD song song AB; AC > CD