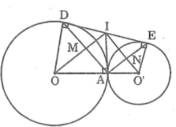
Cho 2 đường tròn (o, 5 cm) và (o, 4 cm) tiếp xúc ngoài tại a. Gọi DE là tiếp tuyến chung của 2 đường tròn, D thuộc (O), E thuộc(O'). Đường thẳng vuông góc với OO' cắt DE tại I.
Tính độ dài DAE
Tính độ dài O'I
Tính độ dài IM( M là trung điểm của OO')
Giải nhanh giúp em tý.