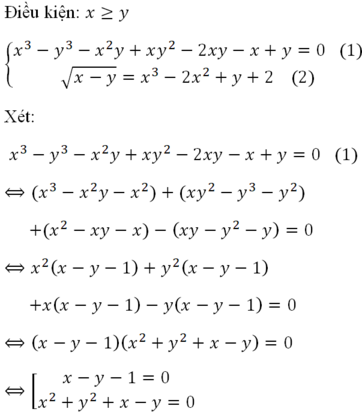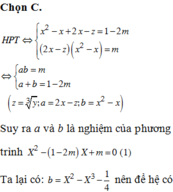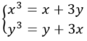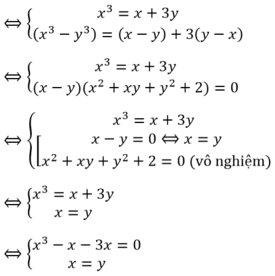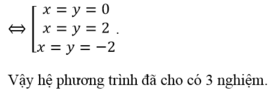Tìm tất cả các nghiệm nguyên x, y của phương trình x3 + 2x2 + 3x + 2 = y3.

Những câu hỏi liên quan
Cho hệ phương trình
x
3
-
y
3
-
x
2
y
+
x
y
2
-...
Đọc tiếp
Cho hệ phương trình x 3 - y 3 - x 2 y + x y 2 - 2 x y - x + y = 0 x - y = x 3 - 2 x 2 + y + 2 Số nghiệm của hệ phương trình là:
A. 2
B. 1
C. 0
D. 3
Tìm tất cả các nghiệm nguyên của phương trình x5-2x4+2x2-(y2+3)x+2y2-2=0
\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
| \(x-2\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(x\) | -6 | -2 | 0 | 1 | 3 | 4 | 6 | 10 |
| \(x^4\) - y2 - 3 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| y | \(\pm\)\(\sqrt{1294}\) | \(\pm\)\(15\) | \(\pm\)1 | \(\pm\)\(\sqrt{6}\) | y2 = -10 (ktm) | \(\pm\)\(\sqrt{249}\) | \(\pm\)\(\sqrt{1291}\) | \(\pm\)\(\sqrt{9996}\) |
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m (biết
m
≥
-
2019
) để hệ phương trình sau có nghiệm thực?
x
2
+
x
-
y
3
1
-
2...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m (biết m ≥ - 2019 ) để hệ phương trình sau có nghiệm thực?
x 2 + x - y 3 = 1 - 2 m 2 x 3 - x 2 y 3 - 2 x 2 + x y 3 = m
A. 2021
B. 2019
C. 2020
D. 2018
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
. Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x
2
m
có 4 nghiệm phân biệt A. -2 m 0 B. -2 ≤ m C. -1 ≤ m D. -1 m 0
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x . Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = 2 m có 4 nghiệm phân biệt
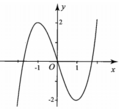
A. -2 < m < 0
B. -2 ≤ m
C. -1 ≤ m
D. -1 < m < 0
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
. Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x
m
2
có 6 nghiệm phân biệt A.
m
∈
-
2...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x . Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = m 2 có 6 nghiệm phân biệt
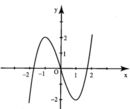
A. m ∈ - 2 ; 0 ∪ 0 ; 2
B. m ∈ 0 ; 2
C. m ∈ - 2 ; 0 ∪ 0 ; 2
D. m ∈ 0 ; 2
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x...
Đọc tiếp
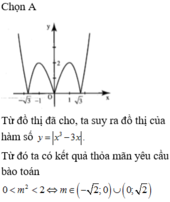
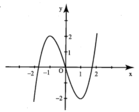
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = m 2 có 6 nghiệm phân biệt.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
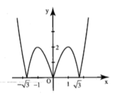
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bào toán ![]()
Đúng 0
Bình luận (0)
Cho phương trình (1+4x-x2).52x^2-3x-1 + (2x2-3x-1).51+4x-x^2 = x2+x. Tổng tất cả các nghiệm của phương trình nằm trong khoảng nào dưới đây?
A.(0;4)
B. (4;6)
C.(6;8)
D. (8;12)
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
64
|
x
|
3
(
x
2
+
1
)
2
(
12
|
x
|
+
m
(
x
2
+
1
)
)...
Đọc tiếp
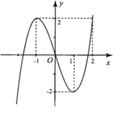
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Đáp án A
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
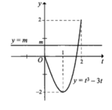
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
x
3
x
+
3
y
y
3...
Đọc tiếp
Số nghiệm của hệ phương trình x 3 = x + 3 y y 3 = y + 3 x là:
A. 2
B. 3
C. 1
D. 4