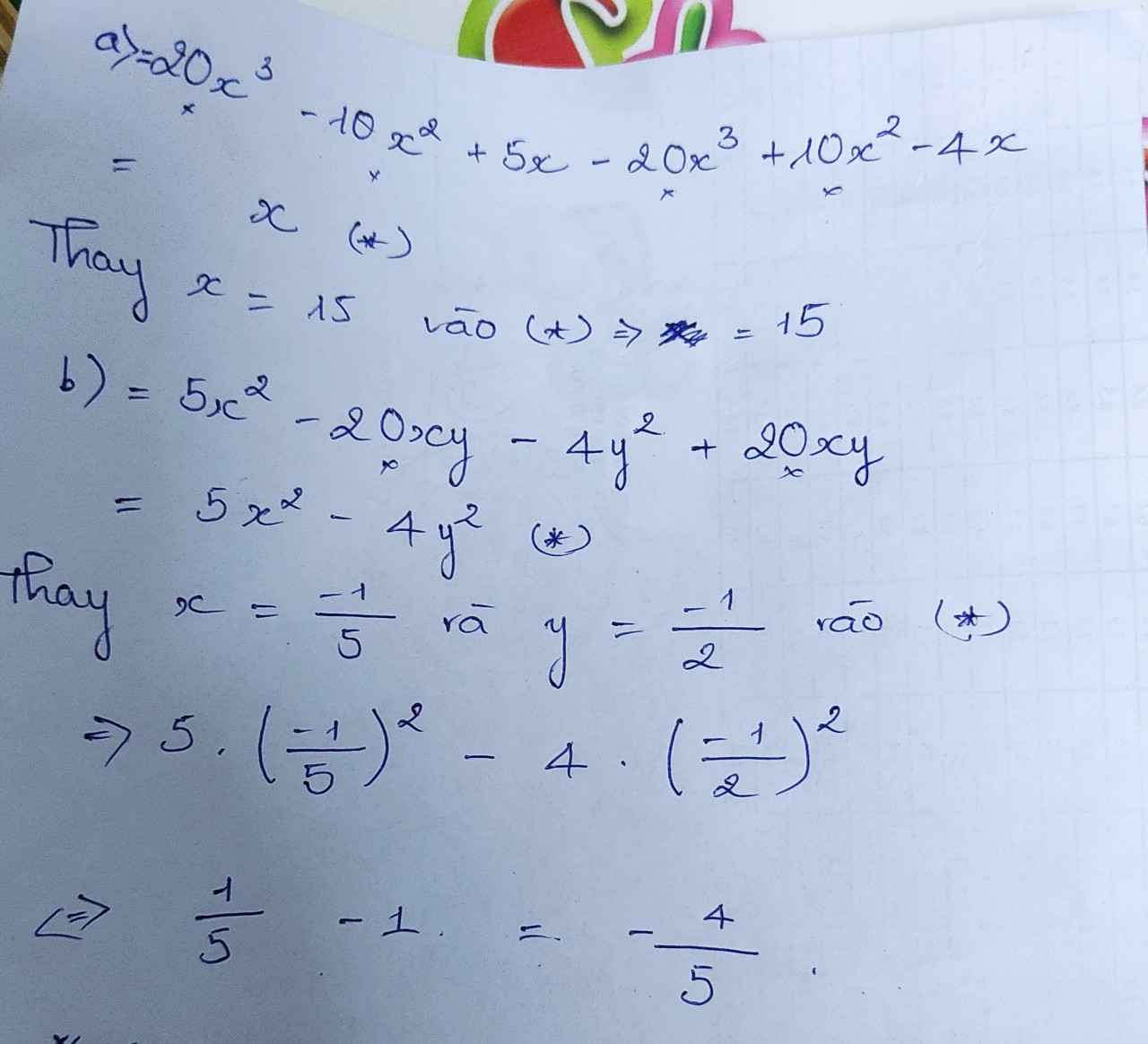Giá trị của x thỏa mãn \(4x\left(5x-1\right)+10x\left(2-2x\right)=16\)là

Những câu hỏi liên quan
Giá trị để x thỏa mãn:\(4x\left(5x-1\right)+10x\left(2-2x\right)=16\) là...........
Bài 1. tính giá trị biểu thức.a. 5xleft(4x^2-2x+1right)-2xleft(10x^2-5x+2right) với x 15b.5xleft(x-4yright)-4yleft(y-5xright) tại xdfrac{-1}{5} và ydfrac{-1}{2}c.6xyleft(xy-y^2right)-8x^2left(x-y^2right)+5y^2left(x^2-xyright)với xdfrac{1}{2};y2giúp mik với mik đang cần gấp cảm ơn
Đọc tiếp
Bài 1. tính giá trị biểu thức.
a. \(5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x+2\right)\) với x = 15
b.\(5x\left(x-4y\right)-4y\left(y-5x\right)\) tại \(x=\dfrac{-1}{5}\) và \(y=\dfrac{-1}{2}\)
c.\(6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2-xy\right)\)với \(x=\dfrac{1}{2};y=2\)
giúp mik với mik đang cần gấp cảm ơn
Giá trị của x thỏa mãn 4x. (5x-1)+10x.(2-2x)=16
1.
giá trị X thỏa mãn 4x*(5x-1)+10x*(2-2x)=16 ?
giá trị x thỏa mãn (x^2+1)*(x^2+5) = ?
Cho các số \(x,y\) thỏa mãn đẳng thức \(5x^2+5y^2+8xy-2x+2x+2=0\). Tính giá trị của biểu thức \(M=\left(x+y\right)^{2007}+\left(x-2\right)^{2008}+\left(y+1\right)^{2009}\)
Đẳng thức: \(5x^2+5y^2+8xy-2x+2y+2=0\)
\(\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Thay vào \(M=\left(x+y\right)^{2007}+\left(x-2\right)^{2008}+\left(y+1\right)^{2009}\) ta được:
\(M=\left(1-1\right)^{2007}+\left(1-2\right)^{2008}+\left(-1+1\right)^{2009}=\left(-1\right)^{2008}=1\)
Đúng 3
Bình luận (0)
Ta có:
\(5x^2+5y^2+8xy-2x+2y+2=0\)
\(\Leftrightarrow x^2+4x^2+y^2+4y^2+8xy-2x+2y+1+1=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2+2y+1\right)+\left(4x^2+8xy+4y^2\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+1\right)^2+\left(2x+2y\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+1\right)^2+4\left(x+y\right)^2=0\)
Mà: \(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\\\left(y+1\right)^2\ge0\\4\left(x+y\right)^2\ge0\end{matrix}\right.\Leftrightarrow\left(x-1\right)^2+\left(y+1\right)^2+4\left(x+y\right)^2\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y+1=0\\x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\\x=-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Thay giá trị x và y vào M ta có:
\(M=\left(x+y\right)^{2007}+\left(x-2\right)^{2008}+\left(y+1\right)^{2009}\)
\(M=\left(1-1\right)^{2007}+\left(1-2\right)^{2008}+\left(-1+1\right)^{2009}\)
\(M=0^{2007}+\left(-1\right)^{2008}+0^{2009}\)
\(M=\left(-1\right)^{2008}\)
\(M=1\)
Đúng 3
Bình luận (0)
tập nghiệm của bất pta) left|4x-8right|le8b) left|x-5right|le4. (số nghiệm nguyên|)c) left|2x+1right| 3x ( giá trị nguyên x thỏa mãn [-2017;2017]d) left|x+1right|+left|xright| 3e) left|2-xright|+3x-1le6
Đọc tiếp
tập nghiệm của bất pt
a) \(\left|4x-8\right|\le8\)
b) \(\left|x-5\right|\le4\). (số nghiệm nguyên|)
c) \(\left|2x+1\right|< 3x\) ( giá trị nguyên x thỏa mãn [-2017;2017]
d) \(\left|x+1\right|+\left|x\right|< 3\)
e) \(\left|2-x\right|+3x-1\le6\)
a, \(\left|4x-8\right|\le8\)
\(\Leftrightarrow\left(\left|4x-8\right|\right)^2\le64\)
\(\Leftrightarrow16x^2-64x+64\le64\)
\(\Leftrightarrow16x^2-64x\le0\)
\(\Leftrightarrow16x\left(x-4\right)\le0\)
\(\Leftrightarrow0\le x\le4\)
b, \(\left|x-5\right|\le4\)
\(\Leftrightarrow\left(\left|x-5\right|\right)^2\le16\)
\(\Leftrightarrow x^2-10x+25\le16\)
\(\Leftrightarrow x^2-10x+9\le0\)
\(\Leftrightarrow1\le x\le9\)
\(\Rightarrow x\in\left\{1;2;3;4;5;6;7;8;9\right\}\)
c, \(\left|2x+1\right|< 3x\)
TH1: \(x\ge-\dfrac{1}{2}\)
\(\left|2x+1\right|< 3x\)
\(\Leftrightarrow2x+1< 3x\)
\(\Leftrightarrow x>1\)
\(\Rightarrow\left\{{}\begin{matrix}x\in Z\\x\in\left(1;2018\right)\end{matrix}\right.\)
TH2: \(x< -\dfrac{1}{2}\)
\(\left|2x+1\right|< 3x\)
\(\Leftrightarrow-2x-1< 3x\)
\(\Leftrightarrow x>-\dfrac{1}{5}\left(l\right)\)
Vậy \(\left\{{}\begin{matrix}x\in Z\\x\in\left(1;2018\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d, \(\left|x+1\right|+\left|x\right|< 3\)
\(\Leftrightarrow x+1+x+2\left|x^2+x\right|< 9\)
\(\Leftrightarrow\left|x^2+x\right|< 4-x\)
Xét hai trường hợp để phá dấu giá trị tuyệt đối
e, Tương tự câu d
Đúng 1
Bình luận (0)
Cho các số x, y thỏa mãn đẳng thức \(5x^2+5y^2+8xy-2x+2y+2=0\). Tính giá trị của biểu thức
\(M=\left(x+y\right)^{2023}+\left(x-2\right)^{2024}+\left(y+1\right)^{2025}\)
\(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>x=1 và y=-1
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}=1\)
Đúng 3
Bình luận (1)
Câu 1: Giá trị của x thỏa mãn
\(\left|x+2,37\right|+\left|y-5,3\right|=0\) là:.....
Câu 2: Giá trị của y thỏa mãn
\(-\left|2x+\frac{4}{7}\right|-\left|y-1,37\right|\) là:....
Câu 1: Giá trị của x thỏa mãn
|x+2,37|+|y−5,3|=0
Để GTBT bằng 0 thì |x+2,37| = 0 và |y−5,3| = 0
-> x = -2,37 , y = 5,3
Vậy x = -2,37
Câu 2: Giá trị của y thỏa mãn
−|2x+\(\frac{4}{7}\)|−|y−1,37| = 0
-> |2x+\(\frac{4}{7}\) = 0 -> x = \(-\frac{2}{7}\)
-> |y−1,37| = 0 -> y = 1,37
Vậy y = 1,37
Đúng 0
Bình luận (0)
Tìm x, biết :
a, \(\left(3x+2\right).\left(6x-2\right)-\left(9x-2\right).\left(2x+1\right)=24\)
b, \(\left(4x+3\right)\left(3x-2\right)-\left(6x-1\right)\left(2x+3\right)=16\)
c, \(\left(5x-2\right)\left(4x+5\right)+\left(10x-7\right)\left(5-2x\right)=12\)
d, \(6x\left(3-4x\right)+8x\left(3x-2\right)=16\)