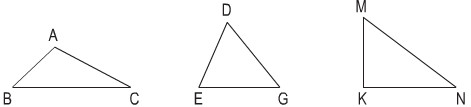
Bài 1. Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
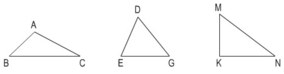
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây: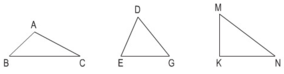
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
Câu 1. Phát biểu nào sau đây sai:
A. Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
B. Nếu hai cạnh và góc của tam giác này bằng hai cạnh và góc của tam giác kia thì hai tam giác đó bằng
nhau.
C. Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam
giác đó bằng nhau.
D. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông
kia thì hai tam giác vuông đó bằng nhau.
Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi :
a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư
b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó
c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông
d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh
Theo định nghĩa ta thấy kết quả:
a) HÌnh trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.
c) Khối nón tròn xoay.
d) Khối trụ tròn xoay.
viets 3 góc 3 cạnh của mỗi hình tam giác dưới đây
các bạn xem sách giáo khoa trang 86 bài 1
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Bộ ba đoạn thẳng nào dưới đây là ba cạnh của một tam giác?
A. 8cm, 8cm, 5cm
B. 1cm, 1cm, 3cm
C. 5cm, 2cm, 1cm
D. 3cm, 2cm, 1cm
Vì 8 + 5 = 13 > 8 thỏa mãn BĐT tam giác nên chọn A
với mỗi bộ ba đoạn thẳng dưới đây bộ ba nào không thể là độ dài ba cạnh của tam giác A 15 ;13 ;16 cm B 2 ;5 ;4 cm C 11; 7; 18 cm D 9 ;6 ;12 cm
Câu nào sau đây sai;
A. Tam giác có hai cạnh bằng nhau và một góc bằng 600 là tam giác đều.
B. Mỗi góc ngoài của tam giác bằng tổng hai góc trong của tam giác đó.
C. Tam giác có độ dài ba cạnh: 12 cm; 13 cm; 5 cm là tam giác vuông.
D. Tam giác có một góc tù là tam giác tù.
GIÚP MÌNH VỚI Ạ MÌNH CẢM ƠN
Bài 31: Cho DABC có AB = 2cm, AC = 5cm, BC = 6cm. So sánh các góc của tam giác ABC.
Bài 32: Cho tam giác DEF có góc E=80, F=30. So sánh các cạnh của ∆DEF.
Bài 33: Trong các bộ ba đoạn thẳng có độ dài sau đây, bộ ba nào là ba cạnh của một tam giác?
a) 4cm; 5cm; 11cm
b) 5dm; 2dm; 7dm
c) 6m; 3m; 5m
Bài 34: Cho tam giác cân có độ dài hai cạnh là 6 cm và 13 cm. Tính độ dài cạnh còn lại và chu vi của tam giác cân đó.
Bài 35: Cho DABC vuông tại A, có AM là đường trung tuyến, biết AB = 6cm, AC = 8cm.
a) Tính AM.
b) Gọi G là trọng tâm của DABC. Tính AG.
Bài 36: Cho tam giác ABC, kẻ AH vuông góc với BC (H Î BC). Biết AC = 20cm; AH = 12cm; BH = 5cm. Tính độ dài HC, AB, BC?
Bài 37: Cho tam giác ABC có góc A=80, góc B=30
a) So sánh các cạnh của tam giác ABC.
b) Vẽ AH vuông góc với BC tại H. So sánh HB và HC
Bài 38: Cho góc nhọn xOy, Ot là tia phân giác của góc xOy, điểm H nằm trên tia Ot. Từ H kẻ HA vuông góc với Ox và HB vuông góc với Oy (A thuộc Ox, B thuộc Oy).
a) Chứng minh tam giác HAB là tam giác cân.
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Chứng minh BC vuông góc với Ox.
c) Khi góc xOy bằng 600, chứng minh OA = 2OD.
Bài 39: Cho tam giác ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K. Chứng minh:
a) Tam giác BNC = Tam giác CMB
b) Tam giác BKC cân tại K
c) BC < 4.KM
Bài 40: Cho tam giác ABC vuông tại A có BD là phân giác, kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của AB và DE. Chứng minh rằng:
a) BD là đường trung trực của AE
b) DF = DC
c) AD < DC
d) AE // FC
Bài 40:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: AD=DE
mà DE<DC
nên AD<DC
d: Ta có: ΔADF=ΔEDC
nên AF=EC
Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
Do đó: AE//CF