Cho tam giác ABC có AB < AC gọi M là trung điểm của BC kẻ AH vuông góc BC tại H trên tia AM lấy D sao cho DM = MA và trên tia AH lấy K sao cho HK = HA
a) AB = CD
b) AB // CD
c) BC là phân giác của góc ABK
Những câu hỏi liên quan
Bài 2. Cho tam giác ABC nhọn có AB AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a) Chứng minh: tam giác AMB tam giác DMCDMC và AB // CDb) Kẻ AH vuông góc BC tại H; DK vuông góc BC tại K. Chứng minh: AH//DK và AH DK.c) Trên tia đối của tia KD lấy điểm E sao cho KE KD.Chứng minh: ME MA.d)Chứng minh: AE//BC.( vẽ hình , ghi giả thuyết , kết luận cho mình nhakk )
Đọc tiếp
Bài 2. Cho tam giác ABC nhọn có AB > AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
.a) Chứng minh: tam giác AMB = tam giác DMCDMC và AB // CD
b) Kẻ AH vuông góc BC tại H; DK vuông góc BC tại K. Chứng minh: AH//DK và AH = DK.
c) Trên tia đối của tia KD lấy điểm E sao cho KE = KD.Chứng minh: ME = MA.
d)Chứng minh: AE//BC.
( vẽ hình , ghi giả thuyết , kết luận cho mình nhakk )
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)
Bài 4: (3,5 điểm)
Cho tam giác ABC có ba góc nhọn ( AB < AC), M là trung điểm của cạnh BC. Trên tia AM lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh: ∆AMB = ∆DMC
b) Chứng minh : AB//CD
c) Kẻ AH vuông góc với BC tại H trên tia AH lấy điểm K sao cho H là trung điểm của AK. Chứng minh MH là phân giác của góc AMK
a/ Xét △ABM và △DMC có:
AM=MD(gt)
MB=MC(gt)
^AMB=^CMD(đối đỉnh)
⇒ΔAMB=ΔDMC(cmt)(đpcm).
b/ Ta có: ΔAMB=ΔDMC(cmt)
⇒^MAB=^MDC⇒^MAB=^MDC[ hai góc ở vị trí so le trong]
Vậy: AB // CD (đpcm).
Đúng 0
Bình luận (0)
cho tam giác nhọn ABC (AB<AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho: MA=MD
a) Chứng minh tam giác MAB = tam giác MDC
b) Chứng minh AB//CD
c) Kẻ AH vuông góc (H thuộc BC). Lấy điểm E sao cho H là trung điểm của AE. Chứng minh BE=CD
a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC (ABAC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MDMA.a) Chứng minh tam giác MABtam giác MDC.b) Kẻ AH vuông góc với BC tại H, kẻ DK vuông góc với BC tại K. Chứng minh: AHDK.c) Trên các đoạn thẳng AB và CD lần lượt lấy điểm E và F sao cho AEDF. Chứng minh: 3 điểm E, M, F thẳng hàng.Mai mình cần ý, vẽ hình giúp mình, mình cảm ơn ạa
Đọc tiếp
Cho tam giác ABC (AB<AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA.
a) Chứng minh tam giác MAB=tam giác MDC.
b) Kẻ AH vuông góc với BC tại H, kẻ DK vuông góc với BC tại K. Chứng minh: AH=DK.
c) Trên các đoạn thẳng AB và CD lần lượt lấy điểm E và F sao cho AE=DF. Chứng minh: 3 điểm E, M, F thẳng hàng.
Mai mình cần ý, vẽ hình giúp mình, mình cảm ơn ạa
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC có AB < AC. Gọi M là Trung điểm của BC. Trên tia đối của tia MA lấy D sao cho DM = MA.
a, cm AB = DC
b, cm AC// BD
c, kẻ AH và DK vuông góc BC tại H và K. Cm HC=KB
Xem chi tiết
Cho tam giác ABC (AB<BC). Gọi M là trung điểm của BC, kẻ AH vuông góc với AC tại H. Trên tia AM lấy D sao cho MD = MA và trên tia đối của tia HA lấy K sao cho HK = HA, CMR:
a)AB = CD
b)AB//CD
c)BC là tia phân giác của góc ABK
các bn giúp mk bài này nha, cảm ơn nhìu lắm
Bài 2. Cho tam giác ABC nhọn có AB AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD MA .a) Chứng minh: tam giác AMB tam giác DMCDMC và AB // CD b) Kẻ AH vuông góc BC tại H; DK vuông góc BC tại K. Chứng minh: AH//DK và AH DK. c) Trên tia đối của tia KD lấy điểm E sao cho KE KD.Chứng minh: ME MA. d)Chứng minh: AE//BC. ( vẽ hình , ghi giả thuyết , kết luận cho mình nhakk ()
Đọc tiếp
Bài 2. Cho tam giác ABC nhọn có AB > AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA .
a) Chứng minh: tam giác AMB = tam giác DMCDMC và AB // CD b) Kẻ AH vuông góc BC tại H; DK vuông góc BC tại K. Chứng minh: AH//DK và AH = DK.
c) Trên tia đối của tia KD lấy điểm E sao cho KE = KD.Chứng minh: ME = MA.
d)Chứng minh: AE//BC. ( vẽ hình , ghi giả thuyết , kết luận cho mình nhakk ()
\(a,\left\{{}\begin{matrix}AM=MD\\BM=MC\\\widehat{AMB}=\widehat{CMD}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABM}=\widehat{DCM}\\ \text{Mà 2 góc này ở vị trí so le trong nên }AB\text{//}CD\\ b,AH\bot BC;DK\bot BC\Rightarrow AH\text{//}DK\\ \left\{{}\begin{matrix}AM=MD\\\widehat{AHM}=\widehat{DKM}=90^0\\\widehat{AMH}=\widehat{KMD}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AHM=\Delta DKM\left(c.g.c\right)\\ \Rightarrow AH=DK\)
Đúng 2
Bình luận (0)
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)
6 tháng 10 2023 lúc 18:02
6. Cho tam giác ABC có AB = AC. Gọi H là trung điểm của BC.
a) CMR: AH là tia phân giác của góc BAC và AH vuông góc BC.
b) Trên tia đối của tia HA lấy điểm K sao cho HK = HA. CMR: CK // AB.
cho tam giác ABC nhọn AB<AC gọi D là trung điểm của BC Trên tia đối của tia DA lấy điểm M sao cho DM=DA a,CMRtam giác ACD=tam giác MBD và AC//BM b,góc ABM= góc MCA c,Kẻ AH vuông góc với BC,MK vuông BC(H,K thuộc BC)lấy E thuộc AH sao cho AE=2/3AH,lấy F thuộc MK sao cho FM=2/3MK.Chứng minh điểm E,D,F thẳng hàng
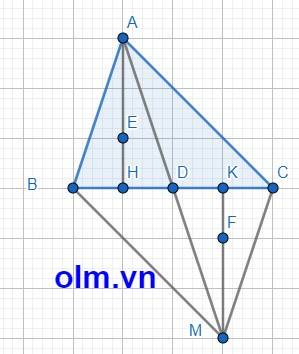
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
Đúng 3
Bình luận (0)
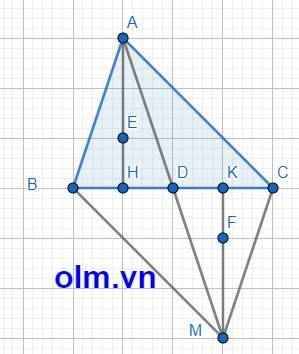
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .
Đúng 0
Bình luận (0)