cho tam giác ABC trên tia đối của AB lấy điểm M sao cho AM=AB trên tia đối của AC lấy điểm N sao cho AC=ĂN
a, CM: MN = BC
b, MN // BC
c,Cm: NB=MC và NB // MC
cho tam giác ABC trên tia đối của AB lấy điểm M sao cho AM=AB trên tia đối của AC lấy điểm N sao cho AC=ĂN
a, CM: MN = BC
b, MN // BC
c,Cm: NB=MC và NB // MC
Các bạn giúp mình hoàn thành bài nha
Cho tam giác ABC trên tia đối của AB lấy điểm M sao cho AM=AB trên tia đối của AC lấy điểm N sao cho AC=AN
a, CM: MN = BC
b, MN // BC
c,Cm: NB=MC và NB // MC
Các bạn giúp mình hoàn thành bài nha
Cho △ABC vuông tại A, AB = 6cm, AC = 8cm.
a) Tính BC
b) Trên tia đối của tia AB lấy điểm M sao cho AM = AC. Trên tia đối của tia AC lấy điểm N sao cho AN = AB. CMR : BC = MN và NB // MC
c) Gọi I là trung điểm MC. CMR: △BIN cân.
a: BC=10cm
b: Xét ΔCAB vuông tại A và ΔMAN vuông tại A có
AB=AN
AC=AM
Do đó: ΔCAB=ΔMAN
Suy ra: CB=MN
cho tam giác ABC. gọi m là trung điểm của AB, N là trung điểm của cạnh AC. trên tia đối của NB lấy điểm D sao cho NB=ND, trên tia đối của tia MC lấy điểm E sao cho MC=ME
a)chứng minh AD=BC
b)chứng minh AE song song với BC
c)chứng minh A là trung điểm của ED
d)gọi H là trung điểm của AD, K là trung điểm của BC. chứng minh N là trung điểm của HK
a: Xét tứ giác ADCB có
N là trung điểm của AC
N là trung điểm của DB
Do đó: ADCB là hình bình hành
Suy ra: DA=BC
Cho tam giác ABC cân tại A. Lấy M, N lần lượt là trung điểm AB, AC. Trên tia đối của tia MC lấy D sao cho DM = MC. Trên tia đối của tia NB lấy E sao cho EN = NB.
a) CM: tam giác ANE = tam giác CNB và suy ra AE // BC
b) CM: tam giác AMD = tam giác BMC.
c) CM: D; A ; E thẳng hàng.
d) CM: DB = EC
e) Lấy K là trung điểm BM. Lấy F thuộc tia đối KC sao cho FK = KC.
(Vẽ hình, chú thích đầy đủ giúp mình nha)
a: Xét ΔANE và ΔCNB có
NA=NC
\(\widehat{ANE}=\widehat{CNB}\)
NE=NB
Do đó: ΔANE=ΔCNB
Suy ra: \(\widehat{AEN}=\widehat{CBN}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
b: Xét ΔAMD và ΔBMC có
MA=MB
\(\widehat{AMD}=\widehat{BMC}\)
MD=MC
Do đó: ΔAMD=ΔBMC
| Cho tam giác ABC vuông tại A , AB = 3 cm ; AC = 4cm |
a) Tính BC
b) Trên tia đối của AB lấy điểm M sao cho AM = AC. Trên tia đối của tia AC
lấy điểm N sao cho AN = AB. Chứng minh BC = MN
c) Chứng minh: NB // MC
d) Gọi I là trung điểm MC. Chứng minh: tam giác BIN cân
a: BC=căn 4^2+3^2=5cm
b: Xét ΔABC vuông tại A và ΔANM vuông tại A có
AB=AN
AC=AM
=>ΔABC=ΔANM
=>BC=NM
c: ΔANB vuông tại A có BA=AN
nên ΔANB vuông cân tại A
=>góc ANB=45 độ
ΔACM vuông tại A có AC=AM
nên ΔACM vuông cân tại A
=>góc ACM=45 độ=góc ANB
=>CM//NB
Cho tam giác ABC có M và N lần lượt là trung điểm của cạnh AB và AC. Trên tia đối của tia NB lấy điểm D sao cho ND=NB. Trên tia đối của tia MC lấy điểm E sao cho ME=MC. Chứng minh:
a) AD=BC
b) AE song song với BC
a: Xet tứ giác ABCD có
N là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AD=BC
b: Xét tứ giác ACBE có
M là trung điểm chung của AB và CE
=>ACBE là hình bình hành
=>AE//BC
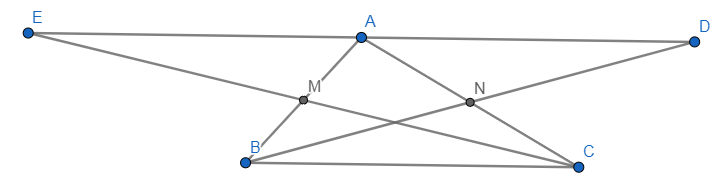
Cho tam giác ABC có M,N lần lượt là trung điểm của cạnh AB và AC. Trên tia đối của tia NB lấy điểm D sao cho ND=NB. Trên tia đối của tia MC lấy điểm E sao cho ME=MC. Chứng minh
A) AD= BC
b) AE// BC
c) >A là trung điểm của DE
\(a,Xét\) \(\Delta ADN\) \(và\) \(\Delta CBN\) \(có:\)
\(NC=NA\\ \widehat{BNC}=\widehat{AND}\\ NB=ND\)
\(\Rightarrow\Delta ADN=\Delta CBN\left(c.g.c\right)\)
\(\Rightarrow AD=BC\) (cạnh tương ứng)
\(b,\Rightarrow\widehat{ADN}=\widehat{NBC}\) (góc tương ứng)
\(\Rightarrow AD\) song song với BC (so le trong)
\(CM:\Delta AME=\Delta BMC\) (bạn tự CM nha)
Từ đó suy ra \(EA=BC\) (cạnh tương ứng) mà BC=AD \(\Rightarrow EA=AD\) (1)
\(\Rightarrow\widehat{AEM}=\widehat{MCB}\) (góc tương ứng)
\(\Rightarrow AE\) song song với BC
Mà \(AE\) song song với BC, AD song song với BC\(\Rightarrow E,A,D\) thẳng hàng (2)
Từ (1) và (2) suy ra A là trung điểm của ED
(đpcm)
Cho tam giác ABC có M,N lần lượt là trung điểm của cạnh AB và AC. Trên tia đối của tia NB lấy điểm D sao cho ND=NB. Trên tia đối của tia MC lấy điểm E sao cho ME=MC. Chứng minh
A) AD= BC
b) góc nhọn AE// BC
c) A là trung điểm của DE
a, Vì \(\left\{{}\begin{matrix}AN=NC\\\widehat{AND}=\widehat{BNC}\left(đối.đỉnh\right)\\BN=ND\end{matrix}\right.\) nên \(\Delta AND=\Delta CNB\left(c.g.c\right)\)
Do đó \(AD=BC\)
b, Vì \(\left\{{}\begin{matrix}AM=MB\\\widehat{AME}=\widehat{BMC}\left(đối.đỉnh\right)\\EM=MC\end{matrix}\right.\) nên \(\Delta AME=\Delta BMC\left(c.g.c\right)\)
Do đó \(\widehat{MAE}=\widehat{MBC}\) mà 2 góc này ở vị trí so le trong nên AE//BC
c, Vì \(\widehat{NAD}=\widehat{NCB}\left(\Delta AND=\Delta CNB\right)\) mà 2 góc này ở vị trí slt nên AD//BC
Mà AE//BC nên A,D,E thẳng hàng
Ta có \(AE=BC\left(\Delta AME=\Delta BMC\right)\)
Mà \(AD=BC\left(cmt\right)\) nên \(AD=AE\)
Vậy A là trung điểm DE