cho 2 đường tròn (O) và (o') bằng nhau cắt nhau tại A và B; kẻ dây AM của (O) và dây BN của (O') sao cho AM//BN. CMR cung nhỏ AM bằng cung nhỏ BN
Những câu hỏi liên quan
Cho 2 đường tròn (O) và (O’) cắt nhau tại 2 điểm A và B. Qua A vẽ dây cung AC của đường tròn (O) cắt (O’) tại C’. Qua B vẽ dây cung BD của đường tròn (O) cắt (O’) tại D’. AC và BD cắt nhau tại I. Chứng minh DC//D’C’.
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
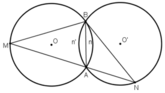
+ (O) và (O’) là hai đường tròn bằng nhau
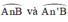cùng được căng bởi dây AB
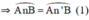
+ (O) có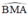 
là góc nội tiếp chắn cung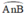 
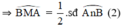
+ (O’) có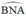 
là góc nội tiếp chắn cung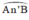 
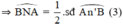
Từ (1); (2); và (3) suy ra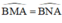 
⇒ ΔBMN cân tại B.
Kiến thức áp dụng
+ Trong cùng một đường tròn hoặc hai đường tròn bằng nhau, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Đúng 0
Bình luận (0)
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
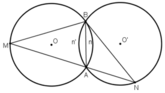
+ (O) và (O’) là hai đường tròn bằng nhau
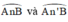cùng được căng bởi dây AB
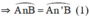
+ (O) có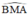 
là góc nội tiếp chắn cung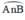 
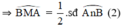
+ (O’) có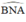 
là góc nội tiếp chắn cung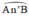 
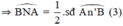
Từ (1); (2); và (3) suy ra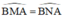 
⇒ ΔBMN cân tại B.
Đúng 0
Bình luận (0)
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra 
= 
(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O) cắt (O') tại C, của đường tròn (O') cắt (O) tại D. AB cắt CD tại M, N là trung điểm CD. Chứng minh góc CAM bằng góc DAN.
Cho đường tròn (O;R) và (O';R/2) tiếp xúc trong tại A. Tia Ot cắt đường tròn O và O' lần lượt tại B và C. Chứng minh 2 cung AB và AC thuộc 2 đường tròn có độ dài bằng nhau
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. (O và O’ nằm ở hai nửa mặt phẳng bờ AB). Một đường thẳng qua A cắt đường tròn (O) và (O’) tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai nửa đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE // KD (E thuộc BD).a) Chứng minh tam giác BOO’ và tam giác BCD đồng dạng.b) Chứng minh tứ giác BCKD nội tiếp.c) Chứng minh AE là tiếp tuyến của đường tròn (O; R).d) Tìm vị trí của CD để diện tích tam giác BCD lớn nhấ...
Đọc tiếp
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. (O và O’ nằm ở hai nửa mặt phẳng bờ AB). Một đường thẳng qua A cắt đường tròn (O) và (O’) tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai nửa đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE // KD (E thuộc BD).
a) Chứng minh tam giác BOO’ và tam giác BCD đồng dạng.
b) Chứng minh tứ giác BCKD nội tiếp.
c) Chứng minh AE là tiếp tuyến của đường tròn (O; R).
d) Tìm vị trí của CD để diện tích tam giác BCD lớn nhất.
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A,B. Vẽ các đường kính AOE, AO'F và BOC. Đường thẳng AF cắt đường tròn (O) tại một điểm thứ hai là D. CMR các cung nhỏ AB, CD, CE bằng nhau
Gợi ý) CM:E,B,F thẳng hàng, BC//AD
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D. Chứng minh C B A ^ = D B A ^
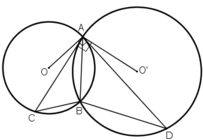
+ Trên đường tròn tâm O:
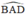là góc tạo bởi tiếp tuyến AD và dây AB
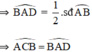
+ Trên đường tròn tâm O’:
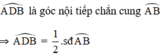
là góc tạo bởi tiếp tuyến AC và dây AB
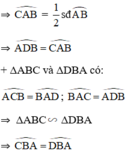
Đúng 0
Bình luận (0)