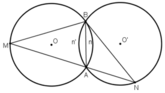
+ (O) và (O’) là hai đường tròn bằng nhau
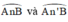 cùng được căng bởi dây AB
cùng được căng bởi dây AB
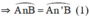
+ (O) có 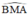 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 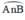
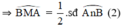
+ (O’) có 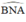 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 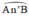
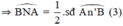
Từ (1); (2); và (3) suy ra 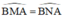
⇒ ΔBMN cân tại B.

+ (O) và (O’) là hai đường tròn bằng nhau
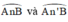 cùng được căng bởi dây AB
cùng được căng bởi dây AB
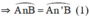
+ (O) có 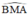 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 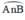
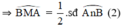
+ (O’) có 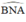 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 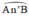
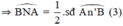
Từ (1); (2); và (3) suy ra 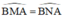
⇒ ΔBMN cân tại B.
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
Cho hai đường tròn (O; R) và (O' R') cắt nhau tại A và H (O và O' ở hai phía của A). Vẽ các đường kính AOB và AO'C của hai đường tròn. Một đường thẳng d qua A cắt đường tròn (O) tại M, cắt đường tròn (O') tại N. A nằm giữa M và N Gọi I, K lần lượt là trung điểm M, N và BC
a. Chứng minh rằng bốn điểm A, H, I, K thuộc một đường tròn.
b. Xác định vị trí của đường thẳng d để diện tích tam giác HMN lớn nhất.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến cắt đường tròn (O) tại C, cắt đường tròn (O') tại D sao cho CD vuông góc với AB, đường thẳng CB cắt đường tròn (O) tại M, đường thẳng DB cắt đường tròn (O') tại N. Chứng minh AB là tia phân giác của góc MAN
Cho (O) và (O) cắt nhau tại A và B, OO'=3cm. Qua A vẽ đường thẳng cắt (O) tại M và cắt (O) tại N (A nằm giữa M và N). Tính độ dài lớn nhất của MN
Cho hai đường tròn (O) và (O') cũng có bán kính là R, cắt nhau tại A và B sao cho O và O' nằm ở hai bên đường thẳng AB. Đường thẳng qua A cắt (O) tại C và cắt (O') tại D sao cho A nằm giữa C và D. Chứng minh BC=BD
Hướng dẫn: vẽ hai đường kính AI của (O) và AK của (O'). Chứng minh B là trung điểm của IK (phải chứng minh I,B,K thẳng hàng). Tứ giác CDKI là hình gì?
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B (O, O’ thuộc hai nửa mặt phẳng bờ AB). Tiếp tuyến chung gần B của hai đường tròn lần lượt tiếp xúc với (O) và (O’) tại C, D. Qua A kẻ đường thẳng song song với CD lần lượt cắt (O) và (O’) tại M, N (M, N khác A). Các đường thẳng CM và DN cắt nhau tại E. Gọi P và Q lần lượt là giao điểm của đường thẳng MN với đường thẳng BC và đường thẳng BD. Chứng minh rằng:a)Đường thẳng AE vuông góc với đường thẳng CD. b)Tứ giác BCED nội tiếp. c)Tam giác EPQ là tam giác cân
Cho hai đường (O) và (O') cắt nhau ở hai điểm A và B. qua A vẽ hai đường thẳng (d) và (d'), đường thẳng (d) cắt (O) tại C và cắt (O') tại D, đường thẳng (d') cắt (O) tại M và cắt (O') tại N sao cho AB là phân giác của góc MAD. Cmr: CD=MN
Cho hai đường (O) và (O') cắt nhau ở hai điểm A và B. qua A vẽ hai đường thẳng (d) và (d'), đường thẳng (d) cắt (O) tại C và cắt (O') tại D, đường thẳng (d') cắt (O) tại M và cắt (O') tại N sao cho AB là phân giác của góc MAD. Cmr: CD=MN
Cho 2 đường tròn O và O' cắt nhau tại A và B. Lấy điểm C nằm giữa A và B. Đường thẳng OC cắt đường tròn O' tại E và D. Qua C kẻ tia Cx vuông góc với OD và cắt đường tròn O tại F. Chứng minh rằng tam giác EDF là tam giác vuông