cho hàm số y=f(x)=x3-4x
a, tinh f(1);f(-1);f(2);f(-2);f(3/2);f(-3/2)
b,so sanh f(a) va f(-a)
giup vs
cho hamf số y=f(x) =4x
a) vẽ đồ thị hàm số
b) tính f(2) , f(-1/2)
Cho hàm số y = f(x) có đạo hàm f'(x) = (x3 - 2x2)(x3 - 2x) với mọi x thuộc R. Hàm số \(\left|f\left(1-2018x\right)\right|\) có nhiều nhất bao nhiêu điểm cực trị?
\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ' ( x ) = x 3 ( x + 1 ) 2 ( x - 2 ) Hàm số y=f(x)có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 0
D. 2
Cho hàm số y=f(x) liên tục trên ℝ , có đạo hàm f ' ( x ) = x 3 ( x − 1 ) 2 ( x + 2 ) . Hỏi hàm số y = f ( x ) có bao nhiêu điểm cực trị?
A. 3
B. 1
C. 0
D. 2
Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.
Cho hàm số y = f ( x ) liên tục trên R, có đạo hàm f ' ( x ) = x 3 ( x - 1 ) 2 ( x + 2 ) . Hỏi hàm số y = f ( x ) có bao nhiêu điểm cực trị
A. 2
B. 0
C. 1
D. 3
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm f'(x) như sau:

Hàm số y = 3 f - x + 2 + x 3 - 9 x + 1 nghịch biến trên khoảng nào sau đây?
A. (−2;1).
B. 2 ; + ∞
C. (0;2).
D. - ∞ ; - 2
Cho hàm số y = f ( x ) liên tục trên R, có đạo hàm f ' ( x ) = x 3 ( x − 1 ) 2 ( x + 2 ) . Hỏi hàm số có bao nhiêu điểm cực trị?
A. 2
B. 0
C. 1
D. 3
Cho hàm số y=f(x) có bảng xét dấu đạo hàm như sau

Hàm số y = f ( 3 x + 1 ) - x 3 + 3 x đồng biến trên khoảng nào dưới đây?
A. 3 4 ; 1
B. 2 3 ; 1
C. 1 4 ; 1 3
D. - 1 ; - 1 3
Ta có y'>0![]()
![]()
Bất phương trình không thể giải trực tiếp, ta sẽ chọn x thoả mãn:
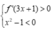
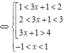
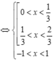
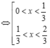
Đối chiếu đáp án chọn C.
Chọn đáp án C.
Cho hàm số y= f( x) Đồ thị hàm số f’( x) như hình bên dưới
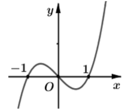
Hàm số y= g(x) = f( x3) đồng biến trên khoảng nào trong các khoảng sau?
A. (-∞; -1)
B. (- 1; 1)
C. (1; + ∞)
D. (0; 1)