cho tam giác ABC có BC lớn nhất. đường tròn tâm I nội tiếp tam giác abc,đường tròn tâm i tiếp xúc BC,CA,AB lần lượt tại D,E,F .qua D kẻ song song AC, cắt EF tại K .chứng minh BE chia đôi DK
Những câu hỏi liên quan
17 tháng 11 2019 lúc 10:51
Một số bài toán hay về tâm nội tiếp:Bài 1: Cho tam giác ABC nội tiếp (O), hai điểm K,L di chuyển trên (O) (K thuộc cung AB không chứa C, L thuộc cung AC không chứa B) thỏa mãn KL song song với BC. Gọi U và V lần lượt là tâm nội tiếp các tam giác AKB,ALC. Chứng minh rằng tâm của (UAV) thuộc đường thẳng cố định.Bài 2: Cho tứ giác lồi ABCD có AD BC. AC cắt BD tại I. Gọi S,T là tâm nội tiếp các tam giác AID,BIC. M,N là trung điểm các cạnh AB,CD. Chứng minh rằng MN chia đôi ST.Bài 3: Cho tam giác AB...
Đọc tiếp
Một số bài toán hay về tâm nội tiếp:
Bài 1: Cho tam giác ABC nội tiếp (O), hai điểm K,L di chuyển trên (O) (K thuộc cung AB không chứa C, L thuộc cung AC không chứa B) thỏa mãn KL song song với BC. Gọi U và V lần lượt là tâm nội tiếp các tam giác AKB,ALC. Chứng minh rằng tâm của (UAV) thuộc đường thẳng cố định.
Bài 2: Cho tứ giác lồi ABCD có AD = BC. AC cắt BD tại I. Gọi S,T là tâm nội tiếp các tam giác AID,BIC. M,N là trung điểm các cạnh AB,CD. Chứng minh rằng MN chia đôi ST.
Bài 3: Cho tam giác ABC, đường tròn (I) nội tiếp tam giác ABC tiếp xúc BC,CA,AB tại D,E,F. Kẻ DH vuông góc EF tại H, G là trung điểm DH. Gọi K là trực tâm tam giác BIC. Chứng minh rằng GK chia đôi EF.
Bài 4: Cho tam giác ABC ngoại tiếp (I), (I) tiếp xúc với BC,CA,AB tại D,E,F. Gọi AI cắt DE,DF tại K,L; H là chân đường cao hạ từ A của tam giác ABC, M là trung điểm BC. Chứng minh rằng bốn điểm H,K,L,M cùng thuộc một đường tròn có tâm nằm trên (Euler) của tam giác ABC.
chị gisp em bài này
Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA lần lượt tiếp xúc đường tròn (I) tại các tiếp điểm là D, E, F. Qua A kẻ đường thẳng song song với BC, đường thẳng này cắt tia EF tại K.a) Chứng minh: AD AK.b) Qua D kẻ đường thẳng song song với BC, đường thẳng này cắt đoạn thẳng EF ở M. Các đoạn thẳng AE và DM cắt nhau ở N. Chứng minh NM ND.
Đọc tiếp
Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA lần lượt tiếp xúc đường tròn (I) tại các tiếp điểm là D, E, F. Qua A kẻ đường thẳng song song với BC, đường thẳng này cắt tia EF tại K.
a) Chứng minh: AD = AK.
b) Qua D kẻ đường thẳng song song với BC, đường thẳng này cắt đoạn thẳng EF ở M. Các đoạn thẳng AE và DM cắt nhau ở N. Chứng minh NM = ND.
Cho tam giác ABC có cạnh BC nhỏ nhất, đường tròn (I) nội tiếp tam giác và tiếp xúc ba cạnh BC,CA,AB lần lượt tại D,E,F. Gọi M,N lần lượt là hai điểm đối xứng của C,B qua E,F. Các đường thảng BM,CN cắt EF lần lượt tại K,L. Chứng minh rằng DK// và D thuộc trung trực của Kl
tam giác ABC có O là tâm đường tròn nội tiếp. E, F, D lần lượt là các tiếp điểm trên AB, BC, CA. Từ O kẻ đường thẳng song song với BC cắt AC tại I. chứng minh AI=BD
Cho đường tròn (I) nội tiếp tam giác ABC. Gọi D, E, F lần lượt là tiếp điểm của BC, CA, AB với (I). Đường thẳng qua A và song song với BC cắt EF tại K. Gọi M là trung điểm của BC. Chứng minh rằng MI vuông góc với DK.
ID cắt EF tại G. cần chứng minh A,G,M thẳng hàng
Ta có : AG cắt BC tại M'. đường thẳng qua G song song với BC cắt AB,AC tại S,T
Dễ thấy \(ID\perp BC\)\(\Rightarrow IG\perp ST\)
Tứ giác FSGI nội tiếp, tứ giác IGET nội tiếp \(\Rightarrow\hept{\begin{cases}\widehat{IFG}=\widehat{ISG}\\\widehat{ITG}=\widehat{IEG}\end{cases}\Rightarrow\widehat{ISG}=\widehat{ITG}}\)( Vì \(\widehat{IFG}=\widehat{IEG}\))
\(\Rightarrow\Delta IST\)cân tại I có \(IG\perp ST\)nên GS = GT
Xét hình thang STCB có BS,M'G,CT cắt nhau tại A và G là trung điểm của ST nên M' là trung điểm của BC
\(\Rightarrow M'\equiv M\)hay A,G,M thẳng hàng
AM cắt KI tại H
Dễ thấy \(AI\perp EF\)nên \(KG\perp AI\)
\(\Delta AIK\)có \(IG\perp AK;KG\perp AI\)nên G là trực tâm \(\Rightarrow AG\perp KI\)tại H
AI cắt EF tại N
Tứ giác ANHK nội tiếp \(\Rightarrow IH.IK=IN.IA=IF^2=ID^2\Rightarrow\frac{IH}{ID}=\frac{ID}{IK}\)
\(\Rightarrow\Delta IDH\approx\Delta IKD\left(c.g.c\right)\)\(\Rightarrow\widehat{IDH}=\widehat{IKD}\)( 1 )
Tứ giác IHMD nội tiếp \(\Rightarrow\widehat{IDH}=\widehat{IMH}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{IKD}=\widehat{IMH}\)
Mà \(\widehat{IMH}+\widehat{MIH}=90^o\)suy ra \(\widehat{IKD}+\widehat{MIH}=90^o\)
\(\Rightarrow MI\perp DK\)
Cho tam giác nhọn ABC (AB<AC) ngoại tiếp đường tròn tâm I. Đường tròn (I) tiếp xúc với các cạnh BC,CA,AB lần lượt tại D,E,F. Đường thẳng EF cắt đường thẳng BC tại M. Đường thằng AD cắt đường tròn (I) tại N(khác D). Chứng minh MN là tiếp tuyến của đường tròn (I).
cho tam giác abc vuông tại a ab lớn hơn ac nội tiếp đường tròn tâm o đường cao ah gọi d là điểm đối xứng với a qua bc gọi k là hình chiếu vuông góc của a lên bc qua h kẻ đường thẳng song song với bc cắt ac tại i đường thẳng bd cắt đường tròn tâm o tại n (n khác b ) tiếp tuyến của đường tròn o tại d cắt đường thẳng bc tại p . chứng minh đường thẳng bc tiếp xúc với đường tròn ngoại tiếp tam giác anp
Đọc tiếp
cho tam giác abc vuông tại a ab lớn hơn ac nội tiếp đường tròn tâm o đường cao ah gọi d là điểm đối xứng với a qua bc gọi k là hình chiếu vuông góc của a lên bc qua h kẻ đường thẳng song song với bc cắt ac tại i đường thẳng bd cắt đường tròn tâm o tại n (n khác b ) tiếp tuyến của đường tròn o tại d cắt đường thẳng bc tại p . chứng minh đường thẳng bc tiếp xúc với đường tròn ngoại tiếp tam giác anp
Cho hình vẽ:Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Đọc tiếp
Cho hình vẽ:
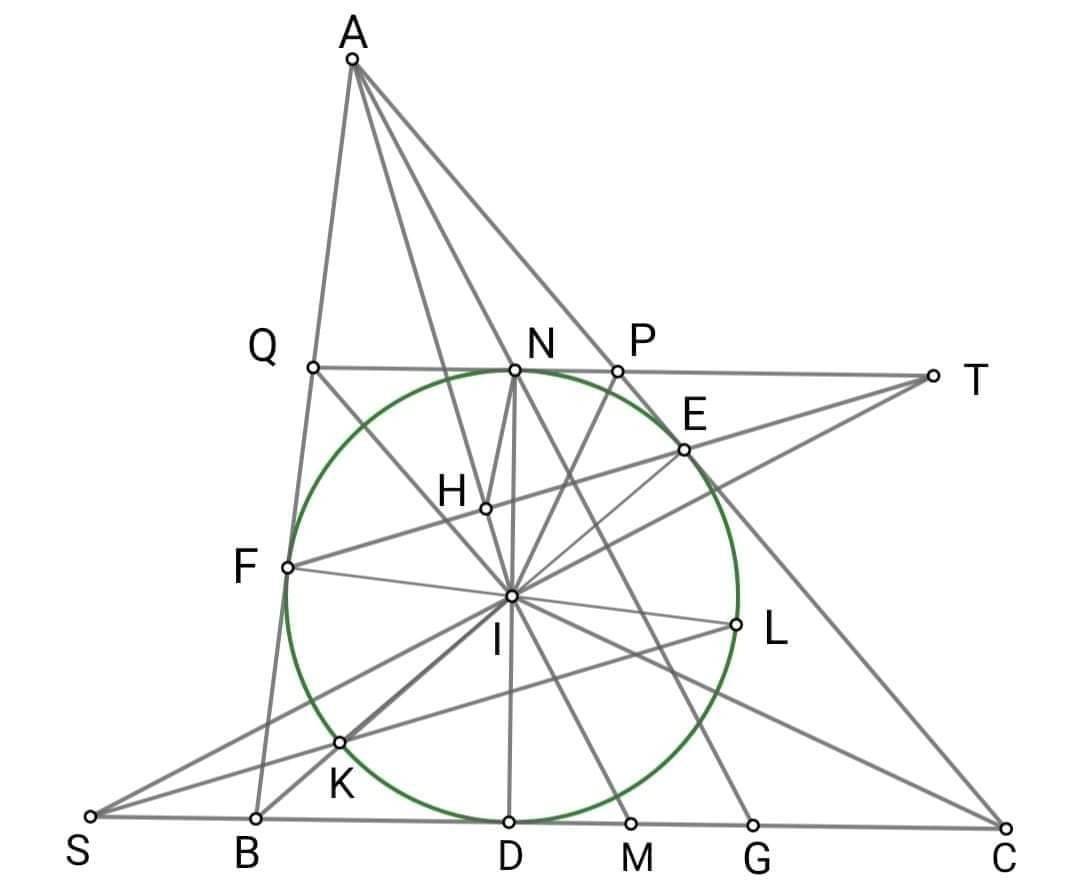Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD = r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
cho tam giác ABC nhọn,đường tròn tâm O,đường kính BC cắt AB, AC tại E và D, CE cắt BD tại H
a)Chứng minh AH vuông góc với BC tại F.
b)Chứng minh tứ giác BEHF nội tiếp.
c)EF cắt đường tròn tâm O tại K (K khác E).Chứng minh DK song song AF
a) Xét tam giác BEC
Ta có :
tam giác BEC nt (O)
BC đường kính
=> tam giác BEC vuông tại E
Xét tam giác BDC
Ta có :
tam giác BDC nt (o)
BC đường kính
=> tam giác BDC vuông tại D
Ta có:
góc BEC vuông tại E
góc BDC vuông tại D
Mà EC cắt DB tại H
=> H là trực tâm
=> AH vuông góc Với BC tại F
c) Xét tg BEHF
Ta có
góc BEH= 90 độ
góc BFH = 90 độ
=> góc BEC + góc BDC = 90 độ + 90 độ = 180 độ
=> tg BEHF nt(tổng 2 góc đối bằng 180 độ )
Ta có: B, E, D, F thuộc (O)
=> tg BEDF nt (O)
=> góc EBD = góc EFD ( 1 )
ta có: tg BEHF nt
=> góc EBH = góc EFH ( 2 )
từ (1) và (2)
=> góc EFD = góc EFH
=> AF // AF
Đúng 0
Bình luận (1)
Cho đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với 3 cạnh BC,CA,AB tại D,E,F. Qua E vẽ đường thẳng song song với BC cắt AD,DF lần lượt tại M,N. CM M là Trung điểm của EN