Cho hàm số y=2x; cho điểm M(2;4); N(0;-1)
Điểm nào thuộc điểm nào không thuộc đồ thị hàm số trên? Vì sao
Những câu hỏi liên quan
Cho hai hàm số y = 2x và y = -2x
Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
- Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
Đúng 0
Bình luận (0)
Cho các hàm số:
(
I
)
y
(
0
,
3
)
-
x
(
I
I
)
y
(
1
,
3
)
-
2
x
(
I
I
I
)
y
4
5
+...
Đọc tiếp
Cho các hàm số:
( I ) y = ( 0 , 3 ) - x
( I I ) y = ( 1 , 3 ) - 2 x
( I I I ) y = 4 5 + 2 x
( I V ) y = e + 1 3 x
Trong các hàm số đã cho, hàm số nào đồng biến trên R ?
A. Chỉ có (I) và (II)
B. Chỉ có (I) và (IV)
C. Chỉ có (IV)
D. Chỉ có (II) và (III)
Chọn B
Hàm số đồng biến khi a > 1.
Viết lại các hàm số về dạng hàm số mũ y = a x :
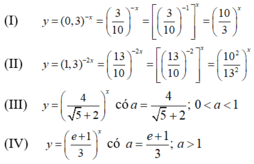
Trong bốn cơ số ta thấy chỉ có hai cơ số lớn hơn 1 là
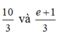
Do đó chỉ có hai hàm số (I) và (IV) là đồng biến trên R
Đúng 0
Bình luận (0)
Cho hai hàm số y = 2x và y = -2x
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
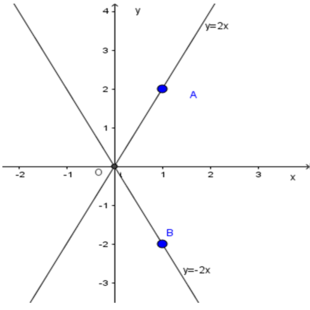
b) - Ta có O ( x 1 = 0 , y 1 = 0 ) và A( x 2 = 1 , y 2 = 2 ) thuộc đồ thị hàm số y = 2x, nên với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) .
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O( x 1 = 0 , y 1 = 0 ) và B ( x 3 = 1 , y 3 = - 2 ) thuộc đồ thị hàm số y = -2x, nên với x 1 < x 3 ta được f ( x 1 ) < f ( x 3 ) .
Vậy hàm số y = -2x nghịch biến trên R.
Đúng 0
Bình luận (0)
Cho hàm số y 2x^2 - 4mx + 5. Tìm giá trị m để hàm số đạt min 5. Tìm giá trị của m để đường thẳng y 5 cắt đồ thị hàm số y 2x^2 - 4mx + 5 tại 2 điểm phân biệt A và B sao cho AB √6
Cho hàm số y2x^2-4mx+5
a) Tìm giá trị m để hàm số đạt min5
b) Tìm giá trị của m để đường thẳng y5 cắt đồ thị hàm số y2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB căn 6
Đọc tiếp
Cho hàm số y = 2x^2 - 4mx + 5. Tìm giá trị m để hàm số đạt min = 5. Tìm giá trị của m để đường thẳng y = 5 cắt đồ thị hàm số y = 2x^2 - 4mx + 5 tại 2 điểm phân biệt A và B sao cho AB = √6
Cho hàm số y=2x^2-4mx+5
a) Tìm giá trị m để hàm số đạt min=5
b) Tìm giá trị của m để đường thẳng y=5 cắt đồ thị hàm số y=2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB= căn 6
a) Tìm giá trị m để hàm số đạt min=5
b) Tìm giá trị của m để đường thẳng y=5 cắt đồ thị hàm số y=2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB= căn 6
Cho đồ thị hàm số
y
-
2
x
như hình vẽ. Hàm số
y
-
2
x
đồng biến trên A. (-∞;0) B. (-∞;0) ∪ (0;+∞) C. R D. (-∞;0) và (0;+∞)
Đọc tiếp
Cho đồ thị hàm số y = - 2 x như hình vẽ. Hàm số y = - 2 x đồng biến trên
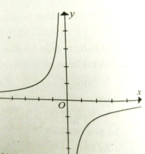
A. (-∞;0)
B. (-∞;0) ∪ (0;+∞)
C. R
D. (-∞;0) và (0;+∞)
Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)
Chọn đáp án D.
Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:
- Không chú ý tập xác định nên chọn đáp án C.
- Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.
Đúng 0
Bình luận (0)
Bải 1: Tìm tập xác định của các hàm số
sau:
a)
3x-2
2x+1
c) y=\sqrt{2x+1}-\sqrt{3-x}
b) y=
²+2x-3
d) y=
√2x+1
X
f(x)
Chú ý: * Hàm số cho dạng v
thi f(x) * 0.
ở Hàm số cho dạng y = v/(x) thì f(r) 2 0.
X
* Hàm số cho dạng " J7(p) thi f(x)>0.
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Đúng 0
Bình luận (0)
Cho hàm số y f(x) 2x + 4a, Tính giá trị của hàm số: f(1) ; f(-1)b, Vẽ đồ thị hàm số: y 2x + 4
Đọc tiếp
Cho hàm số y= f(x) = 2x + 4
a, Tính giá trị của hàm số: f(1) ; f(-1)
b, Vẽ đồ thị hàm số: y = 2x + 4
Cho hàm số
y
x
2
+
2
x
-
3
x
+
2
. Đạo hàm y của hàm số là: A.
1
+
3
x
+
2
2
B.
x...
Đọc tiếp
Cho hàm số y = x 2 + 2 x - 3 x + 2 . Đạo hàm y' của hàm số là:
A. 1 + 3 x + 2 2
B. x 2 + 6 x - 7 x + 2 2
C. x 2 + 4 x + 5 x + 2 2
D. x 2 + 8 x + 1 x + 2 2
Cách 1:
- Ta có:
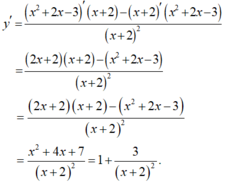
Cách 2:
- Ta có:
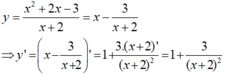
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
3
x
+
5
-
1
+
2
x
. Đạo hàm y’ của hàm số là: A.
7
(
2
x
-
1
)
2
B.
1...
Đọc tiếp
Cho hàm số y = 3 x + 5 - 1 + 2 x . Đạo hàm y’ của hàm số là:
A. 7 ( 2 x - 1 ) 2
B. 1 ( 2 x - 1 ) 2
C. - 13 ( 2 x - 1 ) 2
D. 13 ( 2 x - 1 ) 2
Cho hàm số
y
2
x
-
3
x
-
1
.
Đồ thị hàm số tiếp xúc đường thẳng y 2x + m khi:
A
.
m
8
B
.
m
≠
1
C
.
m
±
2...
Đọc tiếp
Cho hàm số y = 2 x - 3 x - 1 . Đồ thị hàm số tiếp xúc đường thẳng y = 2x + m khi:
A . m = 8
B . m ≠ 1
C . m = ± 2 2
D . ∀ x ∈ R
