giúp với
cho biết sina+cosa=a. tính giá trị của sina.cosa=a^2-m/n với m;n là các số tự nhiên. Tính m-n.
sina và cosa là sin alpha và cos alpha
Những câu hỏi liên quan
Giúp mình với các bạn ơi!!!!!!!!!!!!!!
Cho sina*cosa=0.22. Tính giá trị của biểu thức M=\(\sin^3a+\cos^3a-2.\sin a.\cos a\)
Biết sina.cosa=12/25 , tính sina,cosa (s,i,n,a,c,o là các chữ số)
Biết sina.cosa=12/25 , tính sina,cosa
\(b)\frac{(sina+cosa)^2-(sina-cosa)^2}{sina.cosa}=4\)
chứng minh các hệ thức sau
\(a) \frac{cosa}{1-sina}=\frac{1+sina}{cosa}\)
b) khai triển hằng đẳng thức là ra
a) nhân tích chéo
Đúng 0
Bình luận (0)
\(\frac{\cos\alpha}{1-\sin\alpha}=\frac{1+\sin\alpha}{\cos\alpha}\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha\)\(\Leftrightarrow\cos^2\alpha+\sin^2\alpha=1\)(luôn đúng)
\(\frac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}=\frac{\sin^2\alpha+\cos^2\alpha+2\sin\alpha\cdot\cos\alpha-\sin^2\alpha-\cos^2\alpha+2\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}\)
\(=\frac{4\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}=4\)(đpcm)
Đúng 0
Bình luận (0)
Chứng minh các hệ thức sau :
a) \(\dfrac{cosa}{1-sina}=\dfrac{1+sina}{cosa}\)
b) \(\dfrac{\left(sina+cosa\right)-\left(sina-cosa\right)^2}{sina.cosa}=4\)
a: \(\sin^2a+\cos^2a=1\)
\(\Leftrightarrow\cos^2a=1-\sin^2a=\left(1-\sin a\right)\left(1+\sin a\right)\)
hay \(\dfrac{\cos a}{1-\sin a}=\dfrac{1+\sin a}{\cos a}\)
b: \(VT=\dfrac{\left(\sin a+\cos a+\sin a-\cos a\right)\left(\sin a+\cos a-\sin a+\cos a\right)}{\sin a\cdot\cos a}\)
\(=\dfrac{2\cdot\cos a\cdot2\sin a}{\sin a\cdot\cos a}=4\)
Đúng 0
Bình luận (0)
cho sina+cosa=5/4
a, A=sina.cosa b, B= sina-cosa c,C=sin^3a-cos^3a
help me
\(sina+cosa=\frac{5}{4}\Rightarrow\left(sina+cosa\right)^2=\frac{25}{16}\)
\(\Rightarrow sin^2a+cos^2a+2sina.cosa=\frac{25}{16}\)
\(sina.cosa=\frac{\frac{25}{16}-1}{2}=\frac{9}{32}\)
b/ \(\left(sina-cosa\right)^2=sin^2a+cos^2a-2sinacosa\)
\(\left(sina-cosa\right)^2=1-2.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow sina-cosa=\pm\frac{\sqrt{7}}{4}\)
c/ \(sin^3a-cos^3a=\left(sina-cosa\right)\left(sin^2a+cos^2a+sina.cosa\right)\)
\(=\left(sina-cosa\right)\left(1+\frac{9}{32}\right)=\pm\frac{41\sqrt{7}}{128}\)
Đúng 0
Bình luận (0)
trả lời giúp mk
với ampha nhọn sina-cosa=3/5.tính giá trị biểu thức E=sina.cosa
ampha k viết đc nên viết là a
\(\alpha\) thuộc cung phần tư thứ I
\(sin\alpha-cos\alpha=\frac{3}{5}\)
\(\Leftrightarrow\left(sin\alpha-cos\alpha\right)^2=\frac{9}{25}\)
\(\Leftrightarrow sin^2\alpha-2sin\alpha.cos\alpha+cos^2\alpha=\frac{9}{25}\)
\(\Leftrightarrow sin\alpha.cosa=\)\(\frac{8}{25}\)
Đúng 0
Bình luận (1)
Tính giá trị biểu thức
D=\(\dfrac{cosa+sina}{cosa-sina}\) biết tan α =\(\dfrac{1}{2}\)
Chia cả tử và mẫu cho \(cosa\)
\(D=\dfrac{\dfrac{cosa}{cosa}+\dfrac{sina}{cosa}}{\dfrac{cosa}{cosa}-\dfrac{sina}{cosa}}=\dfrac{1+tana}{1-tana}=\dfrac{1+\dfrac{1}{2}}{1-\dfrac{1}{2}}=3\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức P ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b
π
4
Đọc tiếp
Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b = π 4
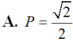
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
Đúng 0
Bình luận (0)
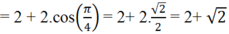
Tính giá trị biểu thức
\(P=\frac{sin^3a+cos^3a}{sina+cosa}\), biết sina.cosa=1
sina.cosa=1 => sina,cosa≠0 => sina+cosa≠0
\(P=\frac{\sin^3a+\cos^3a}{\sin a+\cos a}=\frac{\left(\sin a+\cos a\right).\left(\sin^2a-\sin a.\cos a+\cos^2a\right)}{\sin a+\cos a}\)
\(=\sin^2a+\cos^2a-\sin a.\cos a=1-1=0\)
Đúng 0
Bình luận (0)