Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.

Những câu hỏi liên quan
Nêu vài cách xác định tâm của 1 đường tròn bất kì.
Lấy 3 điểm bất kì thuộc đường tròn đó, nối 3 điểm lại với nhau ta được 1 tam giác. Giao điểm 3 đường trung trực của tam giác chính là tâm đường tròn đó.
Đúng 0
Bình luận (0)
a) (x - 2)(x + 1) = 0\(\Rightarrow\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)
b) (x2 + 7)(x2 - 49) < 0
\(x^2\ge0\Rightarrow x^2+7>0\Rightarrow\hept{\begin{cases}x^2+7>0\\x^2-49< 0\end{cases}\Rightarrow-7< x^2< 49\Rightarrow x^2\in\left\{1;4;9;16;25;36\right\}}\)
\(\Rightarrow x\in\left\{-6;-5;-4;...;4;5;6\right\}\)
c) (x2 - 7)(x2 - 49) < 0 => x2 - 7 và x2 - 49 khác dấu mà x2 - 7 > x2 - 49
\(\Rightarrow x^2-7>0>x^2-49\Rightarrow7< x^2< 49\Rightarrow x^2\in\left\{9;16;25;36\right\}\Rightarrow x\in\left\{-6;-5;-4;-3;3;4;5;6\right\}\)
Đúng 0
Bình luận (0)
x(y + 2) + y = 1
=> x(y + 2) + (y + 2) = 3
=> (x + 1)(y + 2) = 3.Ta có bảng sau :
| x + 1 | -3 | -1 | 1 | 3 |
| y + 2 | -1 | -3 | 3 | 1 |
| x | -4 | -2 | 0 | 2 |
| y | -3 | -5 | 1 | -1 |
Vậy (x ; y) = (-4 ; -3) ; (-2 ; -5) ; (0 ; 1) ; (2 ; -1)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Muốn xác định tâm của 1 đường tròn mà chỉ được dùng ê ke thì phải làm như thế nào?
TK:
Kẻ đường thẳng cắt đường tròn tại A và B.
Qua B, dùng ê ke kẻ đường thẳng vuông góc với AB ở B và cắt đường tròn tại C.
Nối C với A.
Qua A, dùng ê ke kẻ đường thẳng vuông góc với AB tại A và cắt đường tròn tại D.
Nối B với D.
Đúng 3
Bình luận (4)
Ta có các bước làm sau:
Bước 1: Đặt đỉnh góc vuông của 1 ê ke bất kỳ lên đường tròn cho trước
Bước 2: Kẻ đường thẳng chứa cạnh góc vuông của ê ke cắt đường tròn tại 1 điểm, gọi giao điểm đó là B
Bước 3: Kẻ đường thẳng chứa cạnh góc vuông còn lại của ê ke cắt đường tròn tại 1 điểm, gọi giao điểm đó là A
Bước 4: Nối điểm B với điểm A, ta sẽ có đường kính AB
⇒ Bằng 4 bước trên, ta đã xác định được đường kính thứ nhất(đường kính AB) của đường tròn.
+)Để đường kính thứ 2 của đường tròn(gọi là đường kính A’B’), ta sẽ làm tương tự như 4 bước trên. Điều kiện là đường kính A’B’ không trùng với đường kính AB.
⇒ Giao điểm của AB và A’B’ chính là tâm của đường tròn
Đúng 5
Bình luận (0)
Có một miếng sắt hình tròn mà ta chưa biết tâm.Bằng cách nào xác định được tâm của nó
Tìm điểm ở giữa bán kính ! k cho mk nha các bạn !
Đúng 0
Bình luận (0)
đo đường kính của miếng sắt hình tròn .Rồi tìm trung điểm của đường kính vừa đo đc .
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. Lấy AO là đường kính vẽ nửa đường tròn tâm O' cùng phía với nửa đg tròn tâm O. một cái tuyến bất kì qua A giao nửa đường tròn tâm O' và O tại C và D. CMR C là trung điểm AD và tiếp tuyến tại C // với tiếp tuyến tại D.
b*) Nêu cách xác định điểm C sao cho BC là tiếp tuyến (O')
a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. Lấy AO là đường kính vẽ nửa đường tròn tâm O' cùng phía với nửa đg tròn tâm O. một cái tuyến bất kì qua A giao nửa đường tròn tâm O' và O tại C và D. CMR C là trung điểm AD và tiếp tuyến tại C // với tiếp tuyến tại D.
b*) Nêu cách xác định điểm C sao cho BC là tiếp tuyến (O')
a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm
Đúng 0
Bình luận (0)
Thế nào là đường tròn nội tiếp một tam giác? Nêu cách xác định tâm của đường tròn nội tiếp tam giác.
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác.
- Tâm đường tròn nội tiếp tam giác là giao điểm của các tia phân giác của các góc trong của tam giác.
Đúng 0
Bình luận (0)
Thế nào là đường tròn ngoại tiếp một tam giác? Nêu cách xác định tâm của đường tròn ngoại tiếp tam giác.
- Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của các cạnh tam giác.
Đúng 0
Bình luận (0)
Thế nào là đường tròn nội tiếp một tam giác ? Nêu cách xác định tâm của đường tròn nội tiếp tam giác ?
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác. Tâm đường tròn nội tiếp tam giác là giao điểm của các tia phân giác của các góc trong của tam giác.
Đúng 0
Bình luận (0)
Thế nào là đường tròn ngoại tiếp một tam giác ? Nêu cách xác định tâm của đường tròn ngoại tiếp tam giác ?
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của các cạnh tam giác.
Đúng 0
Bình luận (0)
Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy (hình bên). Hãy nêu cách xác định tâm của đường viền.
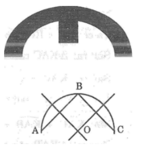
Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực này cắt nhau tại O.
Khi đó; OA = OB = OC
Suy ra: O là tâm của đường viền.
Đúng 0
Bình luận (0)



















