b: Xét ΔAON vuông tại O và ΔAMB vuông tại M co

góc OAN chung

=>ΔAON đồng dạngvới ΔAMB

=>AO/AM=AN/AB

=>AO*AB=AM*AN

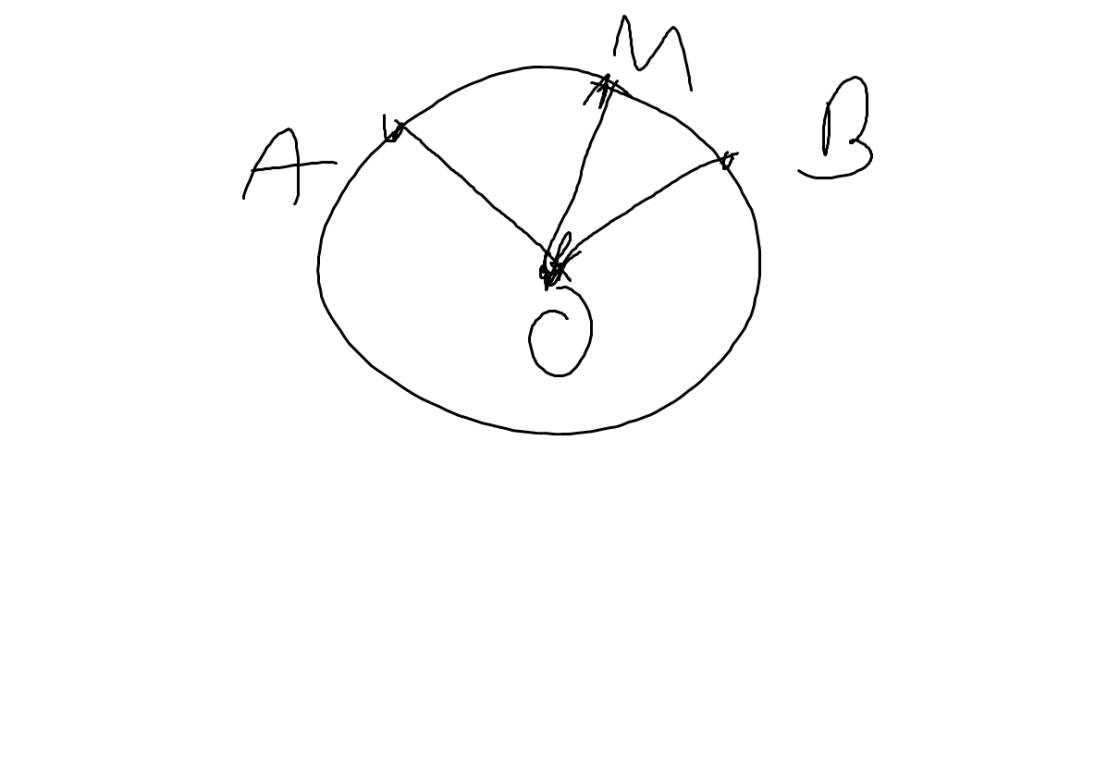
Ta có: M nằm trên cung AB

=>\(sđ\stackrel\frown{AM}+sđ\stackrel\frown{BM}=sđ\stackrel\frown{AB}\)

=>\(sđ\stackrel\frown{BM}=100^0-60^0=40^0\)

a: Ta có: ΔOAM vuông tại A

=>\(OA^2+AM^2=OM^2\)

=>\(AM^2=\left(2R\right)^2-R^2=3R^2\)

=>\(AM=R\sqrt{3}\)

b: Xét ΔMOA vuông tại A có \(sinMOA=\dfrac{MA}{MO}=\dfrac{\sqrt{3}}{2}\)

nên \(\widehat{MOA}=60^0\)

=>\(\widehat{AON}=60^0\)

=>\(\widehat{\left(ON;OA\right)}=60^0\)

c: Xét (O) có

\(\widehat{AON}\) là góc ở tâm chắn cung AN nhỏ

Do đó: \(sđ\stackrel\frown{AN}_{nhỏ}=\widehat{AON}=60^0\)

Số đo cung lớn AN là:

\(360-60=300^0\)

trắc nghiệm thôi..nên giải giúp tôi với ạ^^

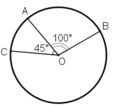
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.

Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.

Do 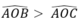 nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.

Suy ra: 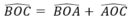 = 1000+ 450 = 1450

Khi đó, số đo cung nhỏ BC là 1450 ( bằng góc ở tâm  )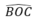

Số đo cung lớn BC là: 3600 - 1450 = 2150

* Trường hợp 2: Điểm C nằm trên cung nhỏ AB

Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB

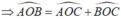
Ta có: 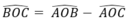 = 1000- 450 = 550

Khi đó, số đo cung nhỏ BC là 550

Số đo cung lớn BC là: 3600- 550 = 3050

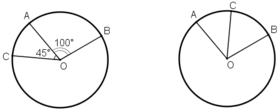
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.

Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.

Do  nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.

Suy ra:   = 100 0 + 45 0 = 145 0

Khi đó, số đo cung nhỏ BC là   145 ° ( bằng góc ở tâm  )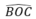

Số đo cung lớn BC là:   360 0 − 145 0 = 215 0

* Trường hợp 2: Điểm C nằm trên cung nhỏ AB

Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB

Ta có:   = 100 0 − 45 0 = 55 0

Khi đó, số đo cung nhỏ BC là  55 0

Số đo cung lớn BC là:  360 0 − 55 0 = 305 0

Kiến thức áp dụng

+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+ Số đo của cung lớn bằng hiệu của 360º và số đo của cung nhỏ (có chung hai mút với cung lớn).

góc AOB=90-36=54 độ

=>sđ cung AB nhỏ=54 độ

sđ cung AB lớn=360-54=306 độ

Xét ΔOAB có OA=OB=AB

nên ΔOAB đều

=>\(\widehat{AOB}=60^0\)

Xét (O) có \(\widehat{AMB}\) là góc nội tiếp chắn cung AB

nên \(\widehat{AMB}=\dfrac{1}{2}\cdot\widehat{AOB}=\dfrac{1}{2}\cdot60^0=30^0\)