Cho biểu thức \(Q=\sqrt[3]{3x^2}\).Tính giá trị của Q khi x = 2 và khi x = − 3 (kết quả làm tròn đến chữ số thập phân thứ hai)

Những câu hỏi liên quan
Tính giá trị của phân thức trong bài tập 62 tại \(x=1,12\) và làm tròn kết quả đến chữ số thập phân thứ ba ?
\(\dfrac{x^2-10x+20}{x^2-5x}\)
Điều kiện của biến .
Ta có
Vì thỏa mãn điều kiện của biến nên khi đó giá trị của phân thức đã cho bằng :
Kết quả chính xác đến 0,001 là
Đúng 0
Bình luận (0)
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):
a) \({\log _3}15\);
b) \(\log 8 - \log 3\);
c) \(3\ln 2\).
a) \(log_315=2,4650\)
c) \(3In2=2,0794\)
Đúng 2
Bình luận (0)
Tính giá trị của phân thức
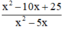
tại x = 1,12 và làm tròn kết quả đến chữ số thập phân thức ba.
Điều kiện xác định: x ≠ 0 và x ≠ 5.
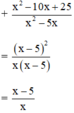
Tại x = 1,12, giá trị phân thức bằng: 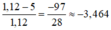
Đúng 0
Bình luận (0)
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
a) \({\log _5}0,5\);
b) \(\log 25\);
c) \(\ln \frac{3}{2}\).
a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)
Đúng 1
Bình luận (0)
Dùng máy tính bỏ túi hoặc bảng số để tìm giá trị gần đúng a của \(\sqrt[3]{12}\) (kết quả được làm tròn đến chữ số thập phân thứ ba). Ước lượng sai số tuyệt đối của a ?
-Kết quả đã làm tròn: 3√12 ≈ 2,289
-Ước lượng sai số tuyệt đối: |2,289 – 2,289| < 0,001
Đúng 0
Bình luận (0)
Cho P(x)=\(\frac{2}{3}x^4-\sqrt{2}x^3+5x+7\)
a) Tìm thương Q(x) khi chia P(x) cho x-5
b) Tìm dư r làm tròn đến chữ số thập phân thứ 3
Câu 1 : Làm tròn số 1,158 đến chữ số thập phân thứ nhất Câu 2 : Tìm tất cả các giá trị của x thỏa mãn |X| = 1/2 Câu 3 : Tìm 2 số x ; y biết: x/3 = y/5 và x+y= - 16 Câu 4 : Số nào dưới đây là số hữu tỉ dương Số 5 : Kết quả của phép tính 2/3 + 7/3 Câu 6 : Tìm x Biết x : (-3)⁴ = (-3)² vậy x = ?
Cho hai số thực dương x, y thỏa mãn: x + y = 5. Tìm gần đúng giá trị nhỏ nhất của biểu thức: P=(x5+5)(y5+5) (Làm tròn kết quả đến 5 chữ số ở phần thập phân)
Thực hiện các phép tính sau trên máy tính bỏ túi :
a) \(\sqrt{3}.\left(0,12\right)^3\) làm tròn kết quả đến 4 chữ số thập phân
b) \(\sqrt[3]{5}:\sqrt{7}\) làm tròn kết quả đến 6 chữ số thập phân
















